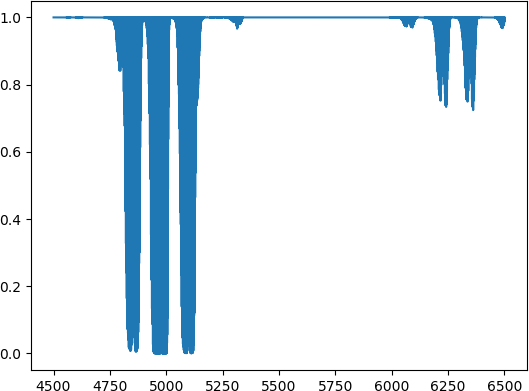
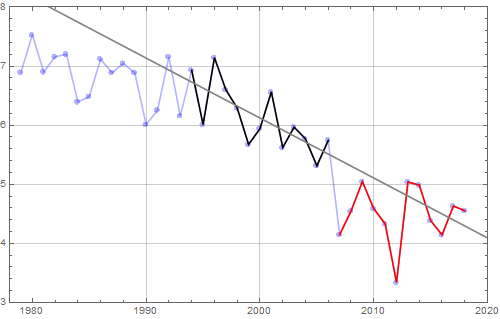
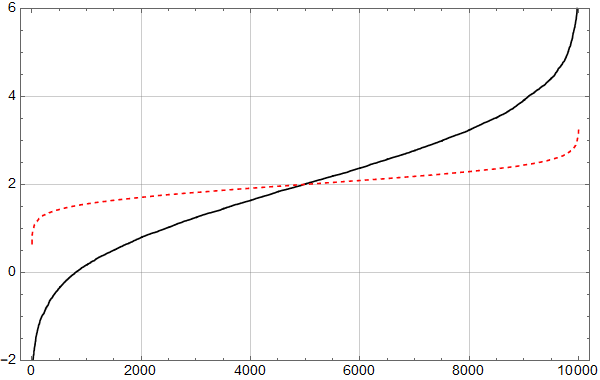
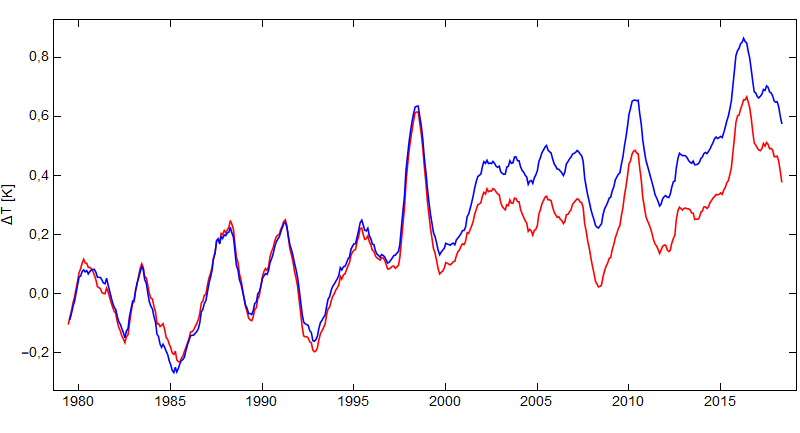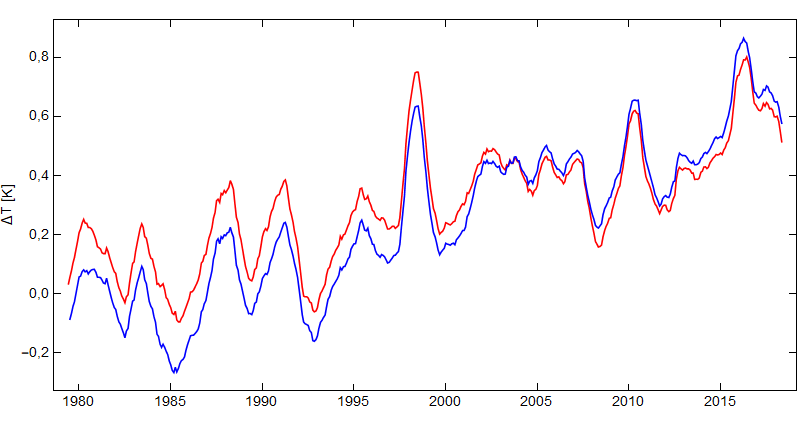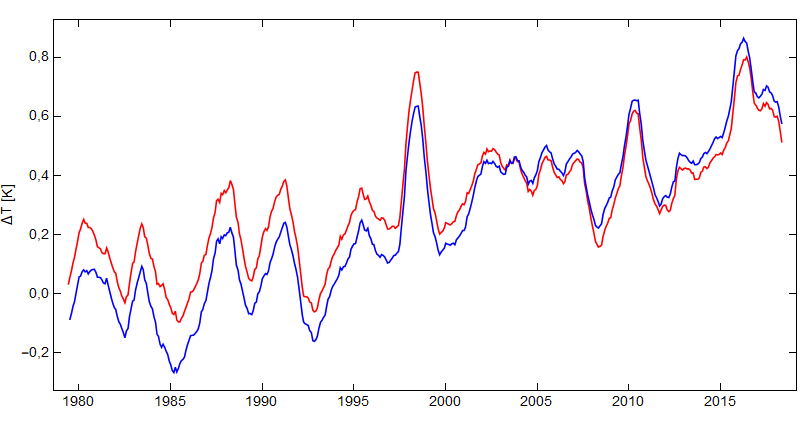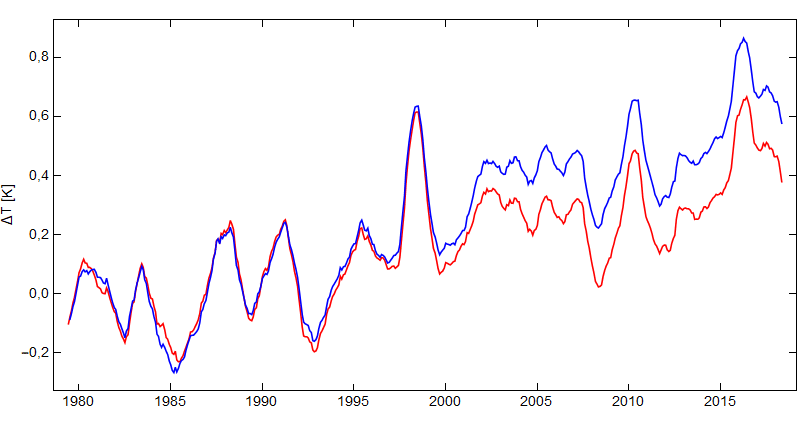
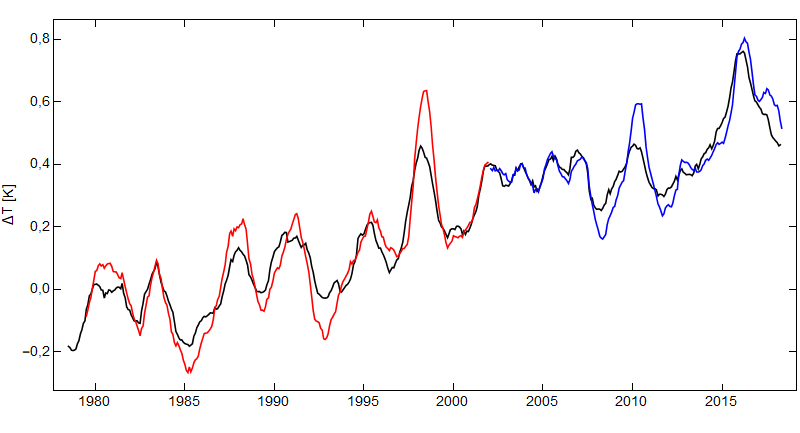
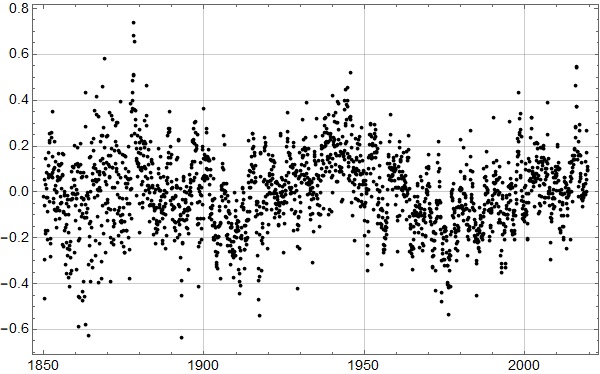
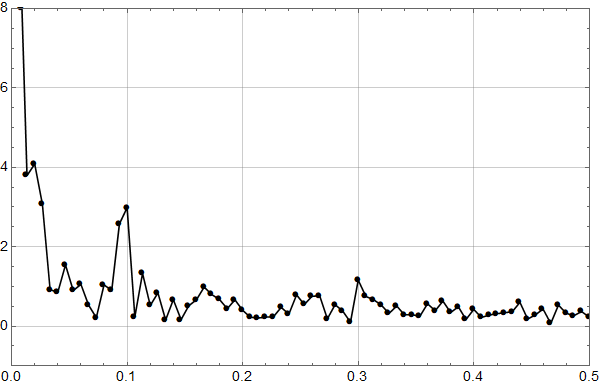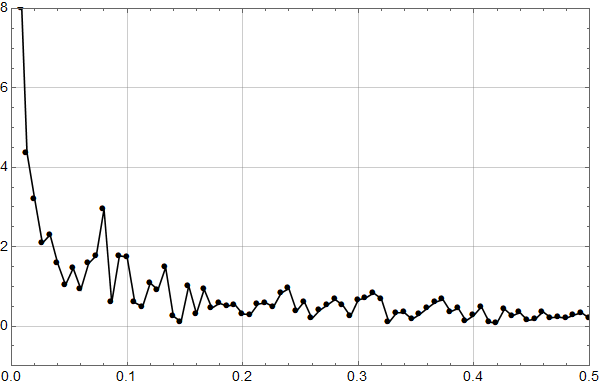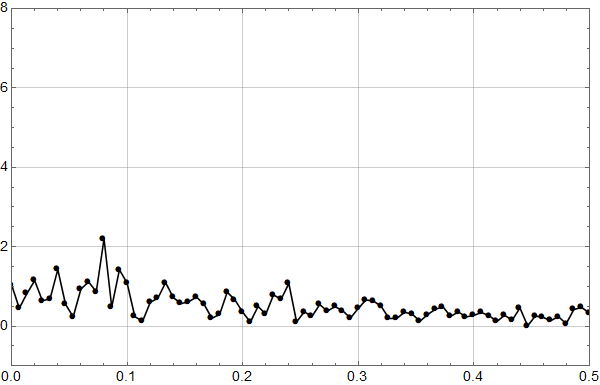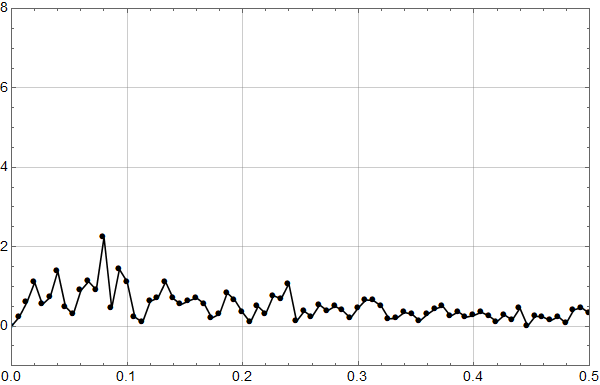Torsdag 19 september 2019 14:58 viste Leif Liland på Terje Wahls blogg denne figuren for HadCrut 3 data.
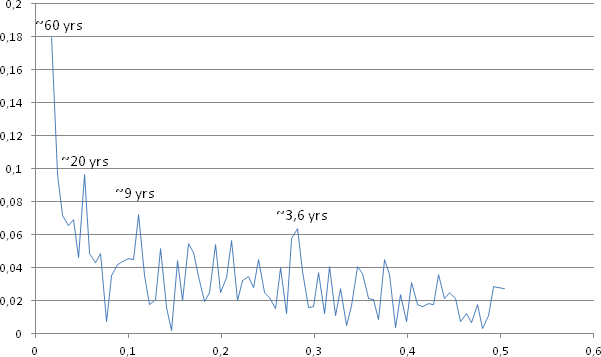
Her er diverse sykler angitt, 60 år, 20 år osv.
Jeg spurte meg derfor: Kan man se sykler i syntetiske data – hvor man vet de ikke finnes?
Men før man går i gang med å Fourier-transformere reelle data, eller syntetiske data som likner på reelle, kan det være greit å se på noen enkle eksempler, for å få en idé om det er fallgruver man kan gå i.
For å følge argumentasjonen under er det nødvendig med litt kjennskap til hvordan svingninger og bølger beskrives med komplekse tall.
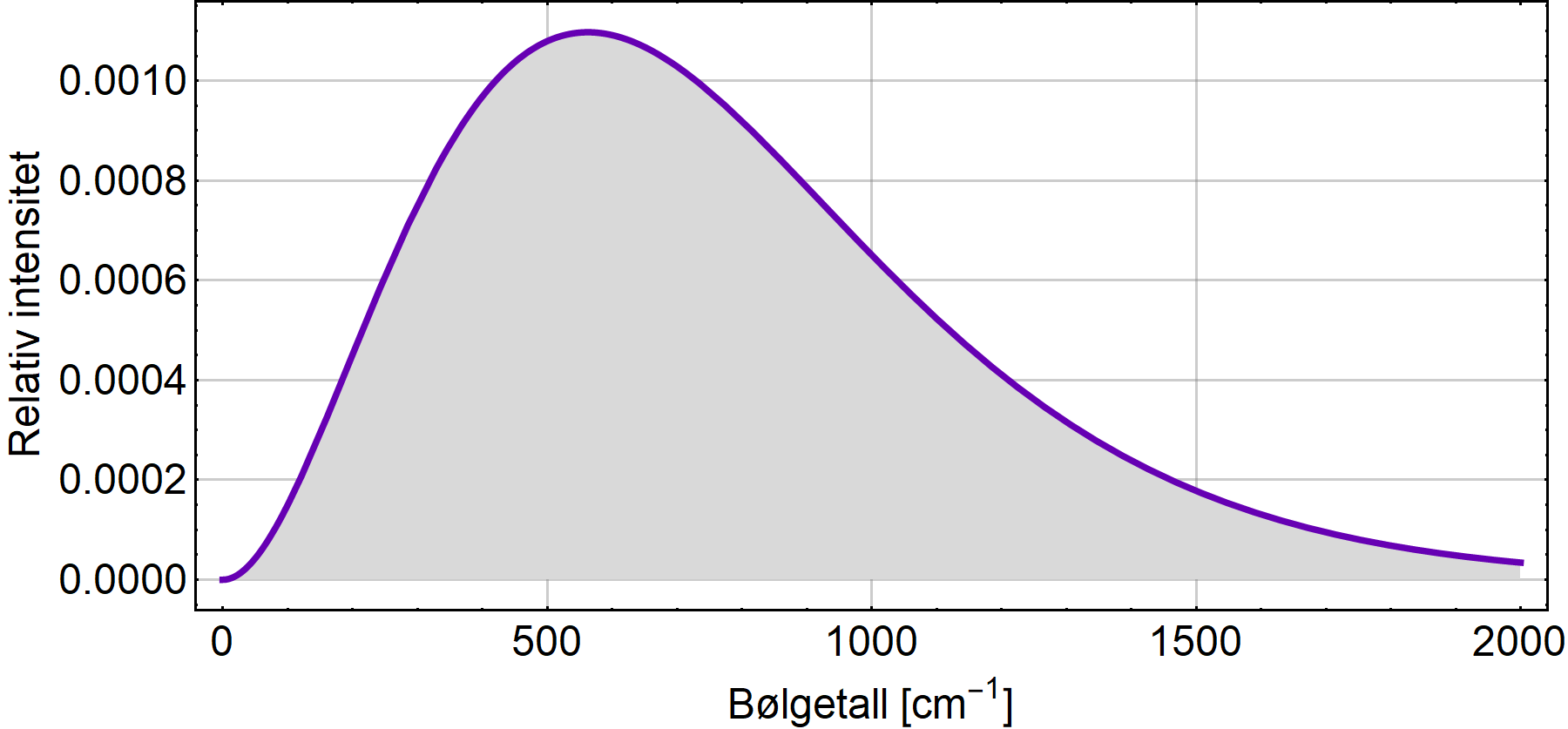
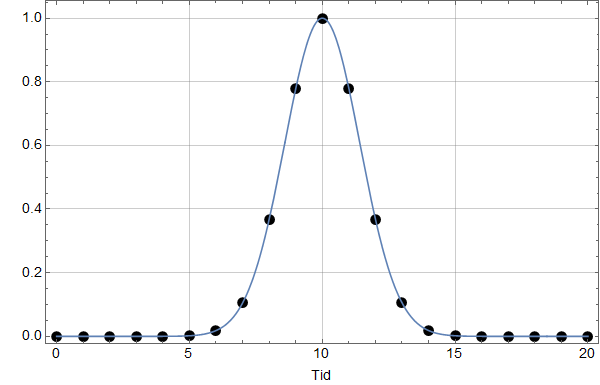
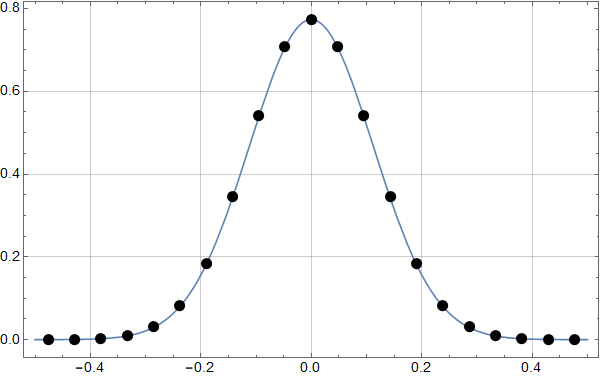
Første figur viser en gauss-puls i tidsplanet som er digitalisert i punkter med lik avstand.
Neste figur viser den Fourier-transformerte slik den vanligvis framstilles. Siden koeffisientene er komplekse tall, har jeg plottet absoluttverdien. Det er like mange punkter som i tidsplanet.
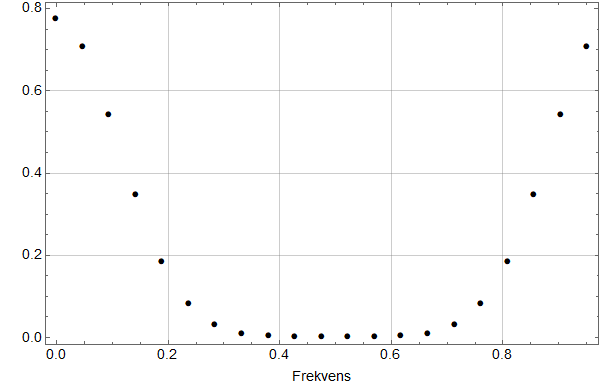
Her kan man undres hvorfor det er frekvenser opp mot 1 – det er jo klart at frekvensene i tidssignalet er lavere. Oppklaringen er at digital Fourier transform (DFT) bare skal regne tilbake for de opprinnelige tids-punktene. Prøver man å beregne mellomliggende punkter direkte basert på DFT-dataene, vil en få komplekse tall.
Siden man kan bare skal «treffe» de opprinnelige punktene kan man multiplisere med et signal som har samme verdi i alle punktene – en sinus som gjør en hel eller flere hele perioder mellom hvert opprinnelige punkt i tidsplanet.
I praksis betyr det at man kan flytte de digitale punktene opp eller ned (en eller flere ganger) med totalt antall punkter.
Det mest logiske er å flytte øvre halvdel nedover. Da får man et signal som er symmetrisk om null frekvens, som vist i neste figur. Den heltrukne kurven er en gaussisk puls – som er i tråd med at den Fourier transformerte av en gaussisk puls er en gaussisk puls i frekvensplanet.
I dette plottet er koeffisientene for en positiv og tilhørende negativ frekvens de kompleks konjugerte av hverandre. Det betyr at når de summeres får man alltid et reelt signal, og man kan bruke dataene på denne formen til å interpolere mellom de opprinnelige punktene i tid.
Koeffisienten for null frekvens er reell, og er et mål for middelverdien av signalet i tidsplanet.
På grunn av symmetrien mellom positive og negative frekvenser, kan vi nøye oss med å plotte de positive. Det gjøres i det følgende.
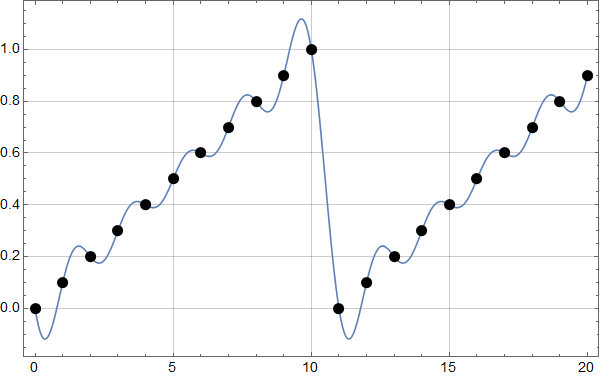
Neste figur viser en hel periode av en sinus-kurve med frekvens 0,1, digitalisert med 11 punkter med samme avstand.
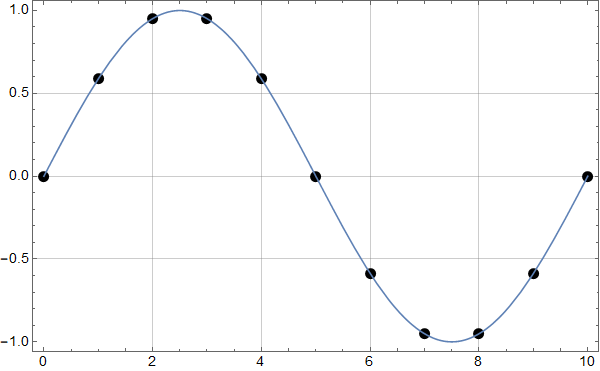
Den digitale Fourier-tranformasjonen ser slik ut:
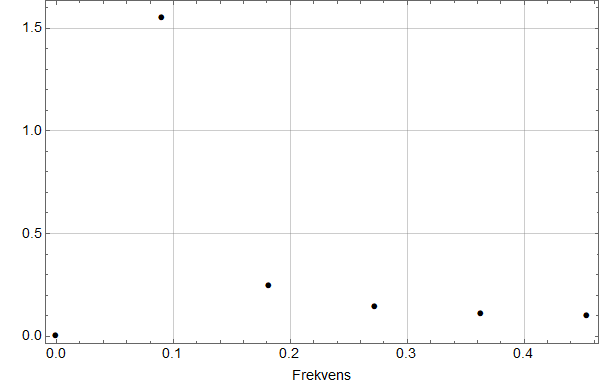
Her er det flere ting som i første omgang kan se overraskende ut: Vi har ikke noe punkt på 0,1 – frekvensen til sinusbølgen, og det er flere andre frekvenser som også er ulik null.
Oppklaringen er enkel, men vesentlig: Hver enkelt frekvens beskriver en uendelig sinusfunksjon. Men et endelig antall frekvenser kan man bare beskrive en periodisk funksjon, dvs en funksjon som gjentar seg selv om og om igjen.
Vi ser at dataene både starter og slutter med en null. Når vi gjør dette periodisk, får vi 2 nuller på rad: Vi har ikke lenger en ren sinus.
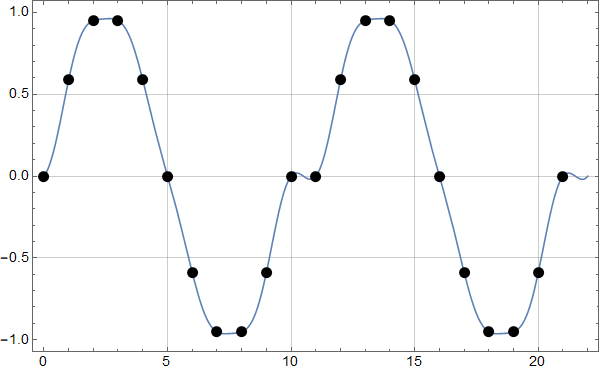
Neste figur viser punktene for 2 perioder, og med blått viser resultatet av den inverse fourier-transformasjonen, også for mellomliggende punkter. Det er tydelig at dette ikke er en ren sinus – noe som stemmer med at vi hadde flere frekvenser ulik null.
Ved å droppe det siste punktet, får vi en sekvens som kan skjøtes sammen til en ren sinus.
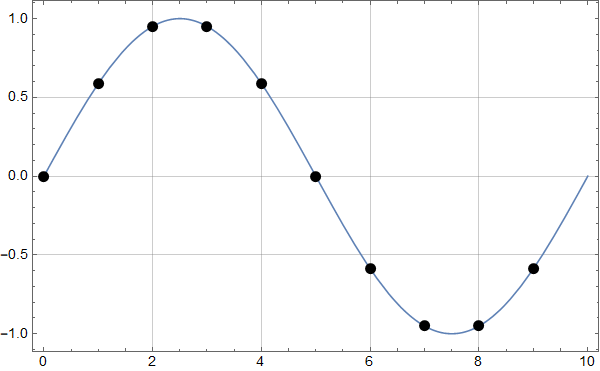
Og ganske riktig: Vi får da bare én frekvens, den riktige på 0,1.
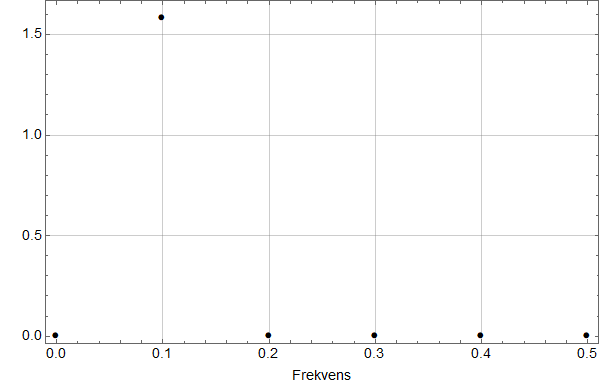
Dette er et viktig poeng: En digital Fouriertransform antar implisitt at tidssekvensen den brukes på er periodisk!
La oss se hvordan det virker for en lineært økende kurve – som Fouriertransformasjonen altså ser på som en periodisk sag-tann kurve. Den stiger jevnt, men faller brått tilbake til startpunktet for hver periode.
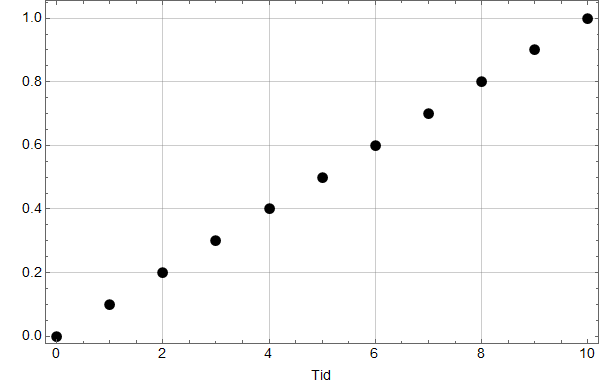
her er den digitale Fourier transformasjonen
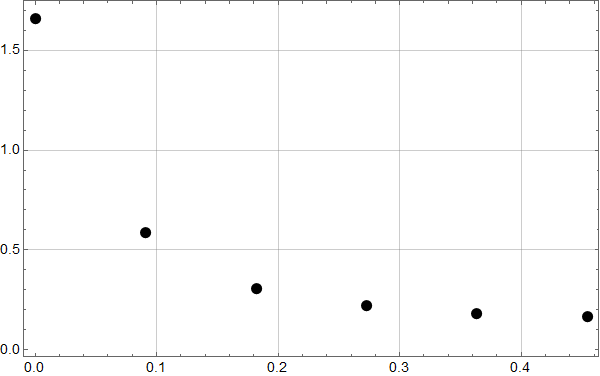
og neste figur viser hvordan Fourier dataene med interpolasjon blir i tidsplanet, for 2 perioder. De opprinnelige dataene vises som svarte punkter.
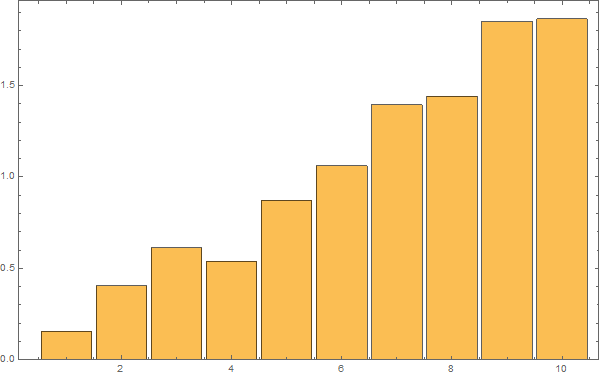
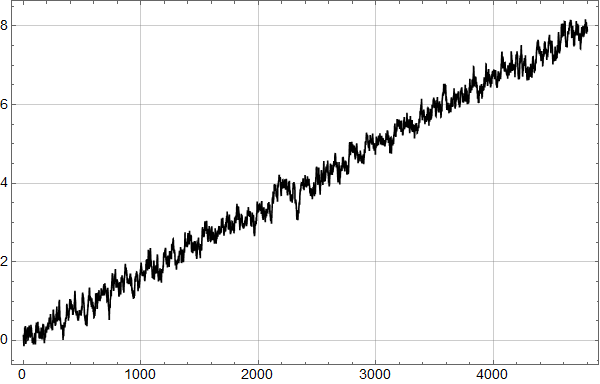
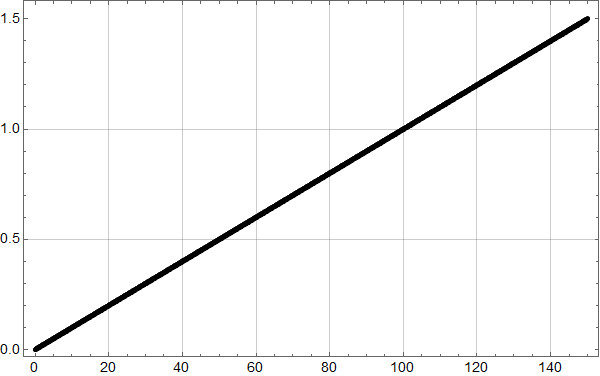
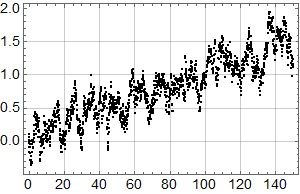
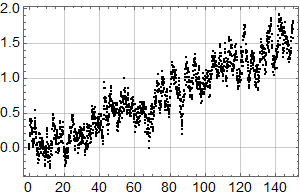
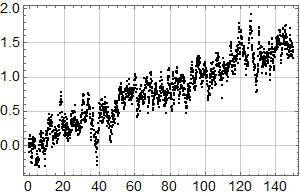
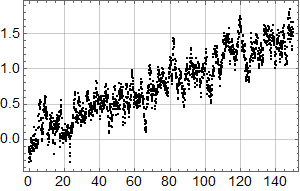
La oss så se på en dataserie med månedlige data over 150 år, som stiger til sammen 1,5 grader:
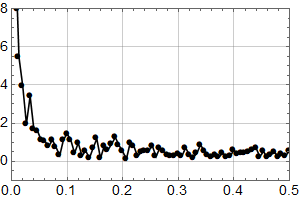
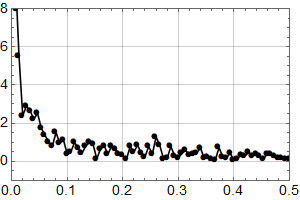
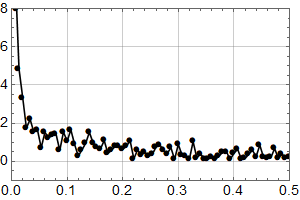
Den Fourier transformerte (opp til f=0.5 per år) er (punktet for f=0 faller utenfor plottet – det er middelverdien og dermed ikke så interessant).
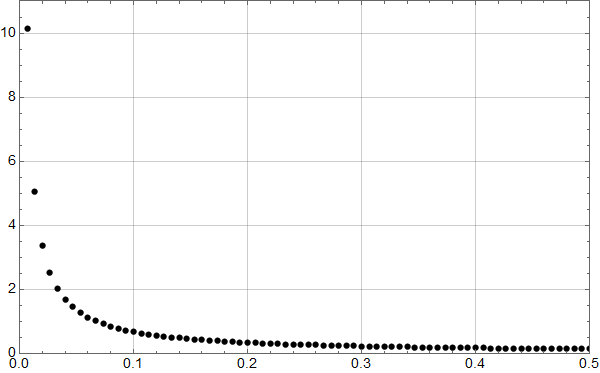
Man kjenner igjen økningen under 0,1 fra det første plottet for HadCrut 3 dataene!
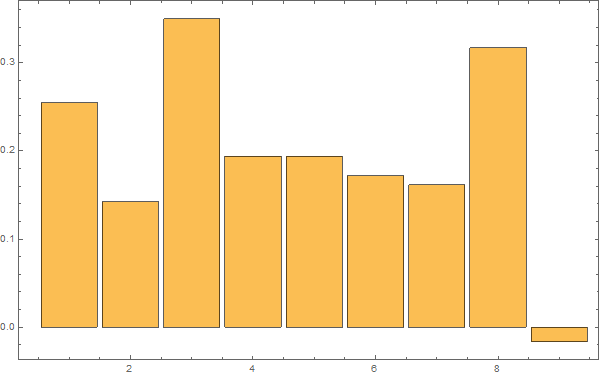
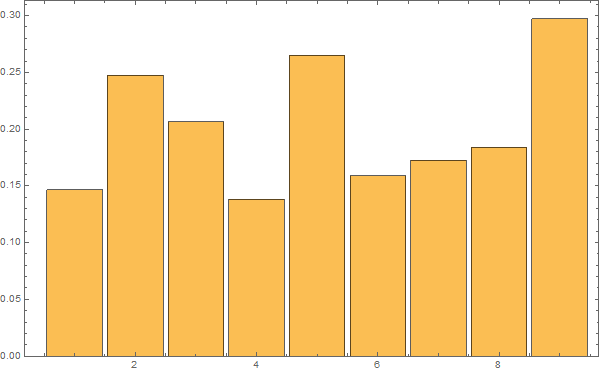
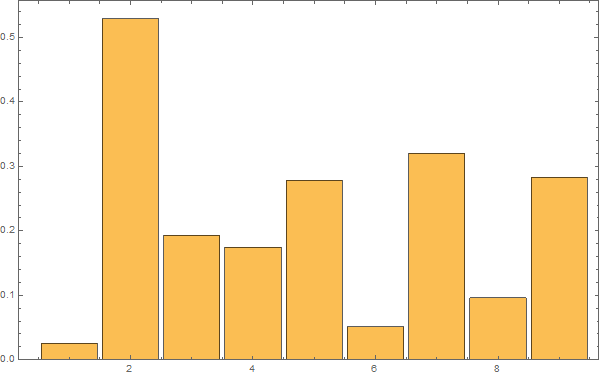
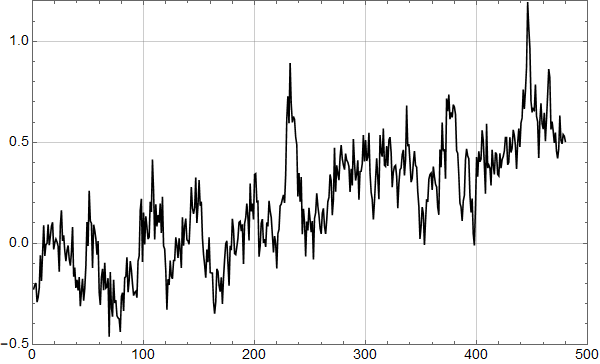
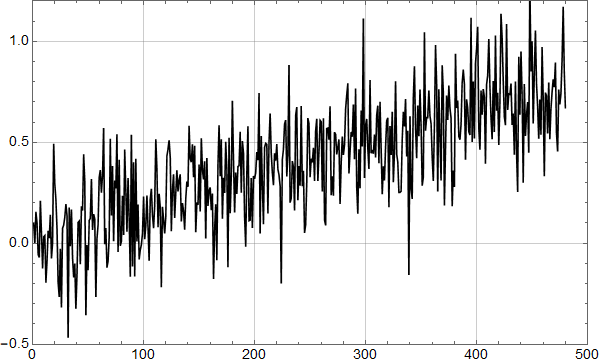
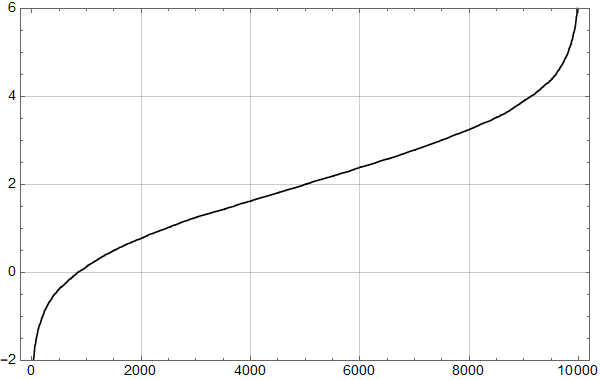
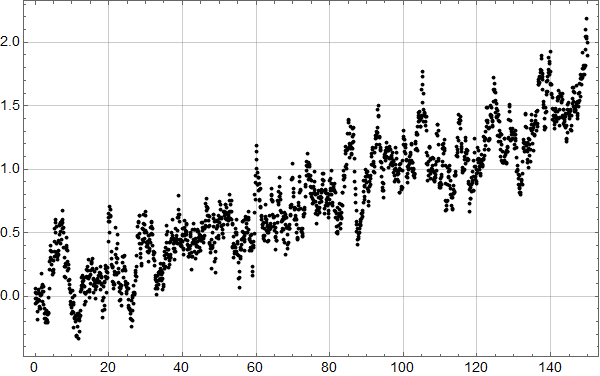
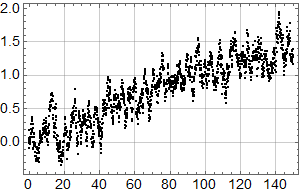
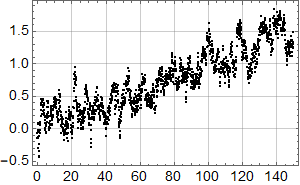
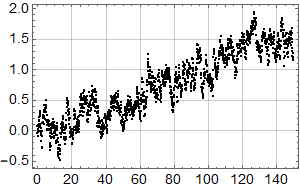
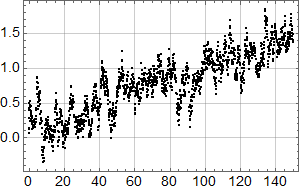
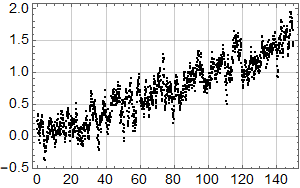
Etter denne innledningen er man bedre rustet til å se på syntetiske data. Her er 3 realisasjoner av en AR(1) prosess med lineær stigning 1 grad per hundre år samt støy med autokorrelasjonskoeffisent 0,92 og standardavvik 0,2:
Realisasjonene er ikke tilfeldig valgt – jeg har sett etter eksempler som likner de reelle dataene. Men se helt nederst for 10 tilfeldige realisasjoner.
Realisasjon 1:
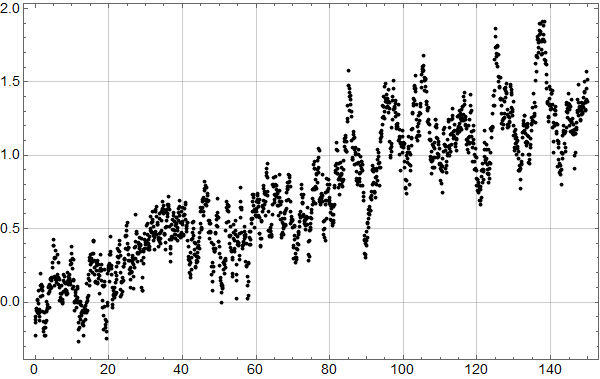
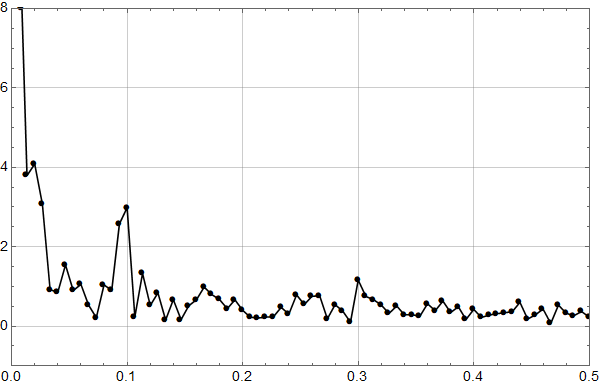
Realisasjon 2:
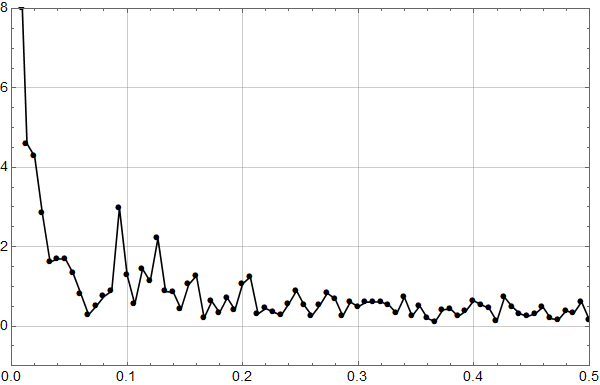
Realisasjon 3:
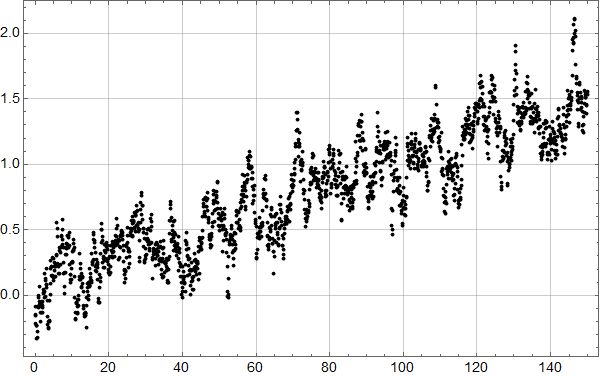
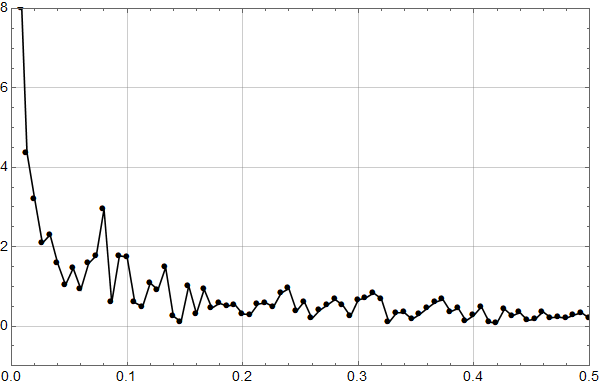
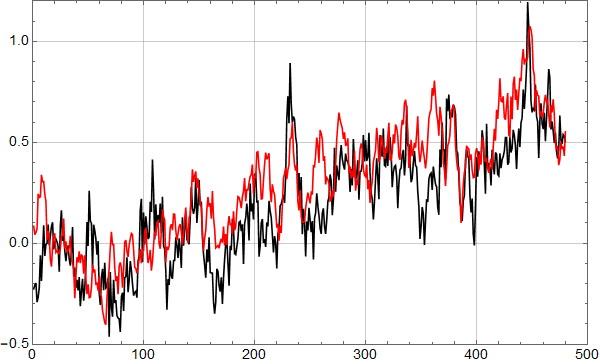
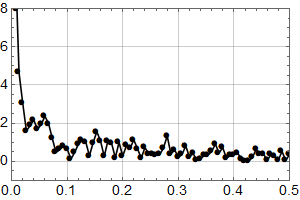
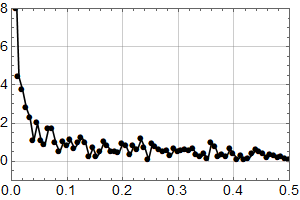
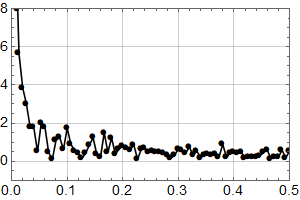
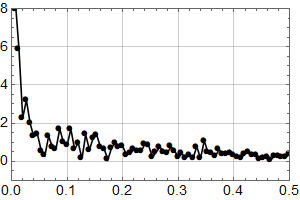
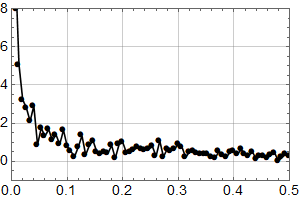
Vi ser at kurvene øker mot null frekvens som for den lineære uten støy, og man ser at kvalitativt kan man tolke omtrent like mye sykler som i HadCrut3 dataene vi startet med. Men vi vet altså med sikkerhet at det ikke er deterministiske sykler i de syntetiske dataene – kun tilfeldig statistisk variasjon.
Konklusjonen må bli at man ikke kan konkludere sikkert med sykler fra HadCrut 3 plottet heller.
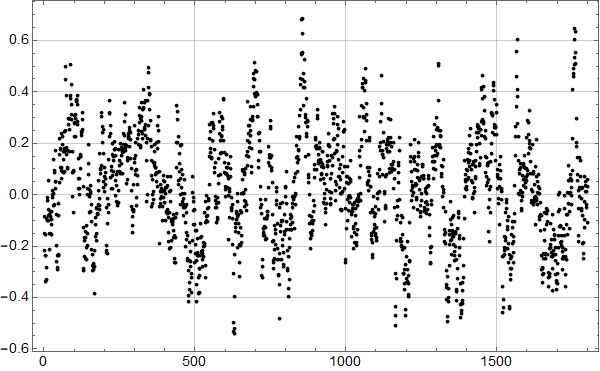
De neste figuren viser hvordan det går når vi fjerner den underliggende trenden i realisasjon 3.
Først bruker vi trenden som ble brukt da dataene ble generert:
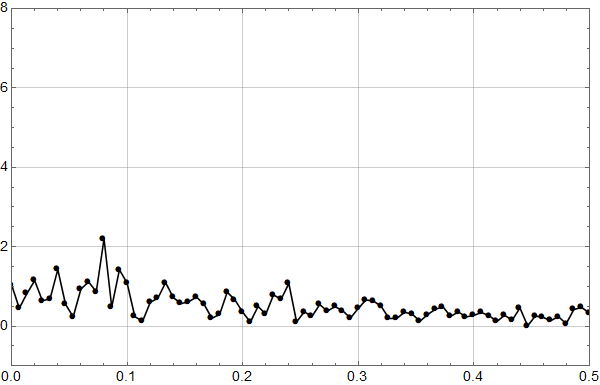
Man ser at stigningen mot null frekvens er borte.
Neste 2 plott viser hvordan det går når man bruker lineær trend bestemt med minste kvadraters metode. Forskjellen er ubetydelig – som man kunne vente.
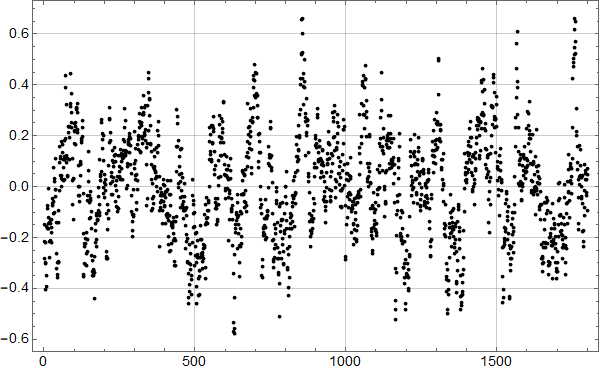
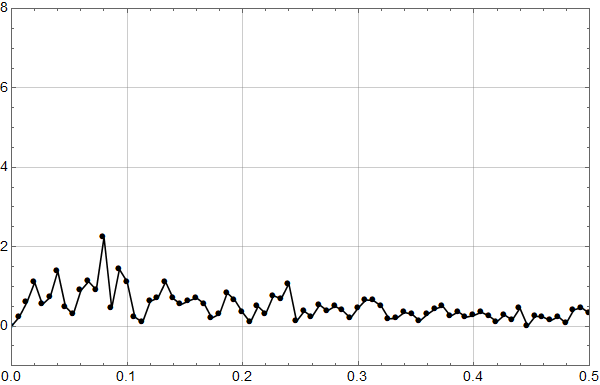
Hva så med HadCrut 4?
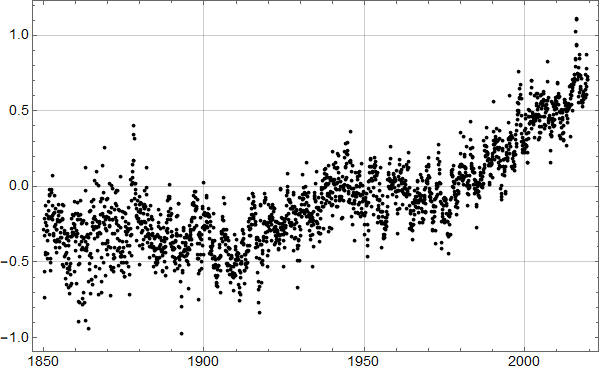
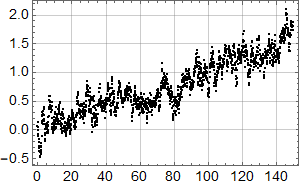
Neste figur viser globale HadCrut4 data lastet ned fra WoodForTrees 1. oktober 2019.
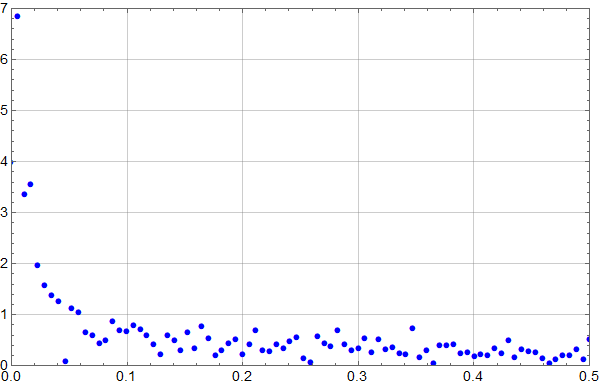
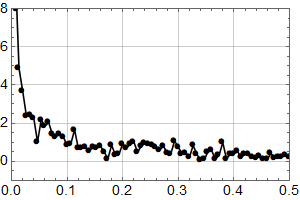
Neste figur viser spekteret. Ingen helt åpenbare sykler, men vi ser den ventede stigningen mot null frekvens – den er et resultat av differensen mellom 2019 og 1850.
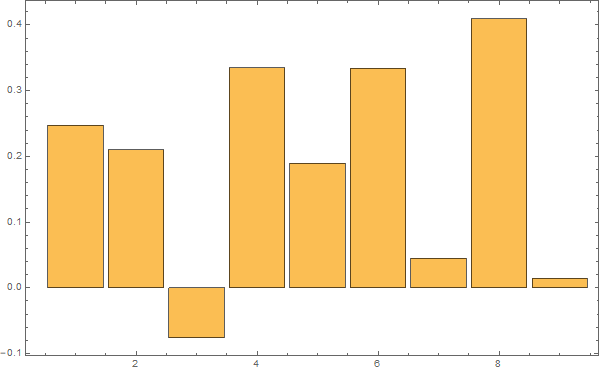
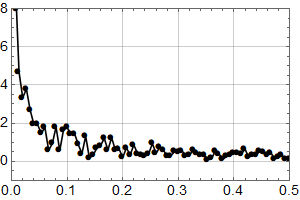
Det er klart at dataene ikke kan beskrives godt med en lineær underliggende trend. Her er et forsøk med en kvadratisk tilpasning:
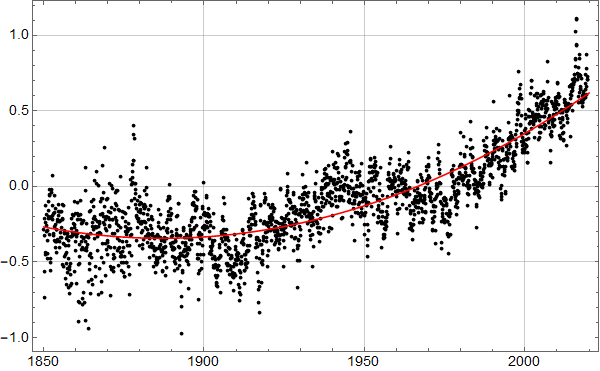
Residual-dataene blir da slik:
med frekvens-spektrum som dette:
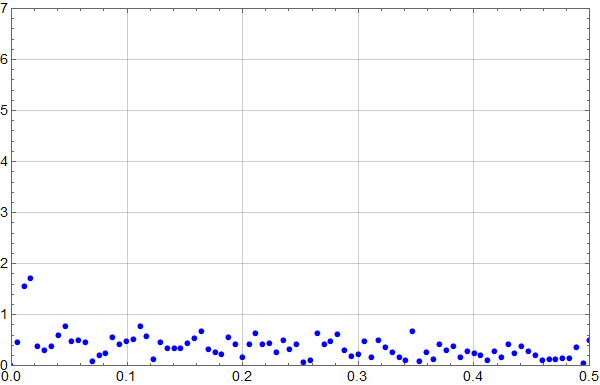
Både tidsplottet og frekvensplottet antyder «noe» med en periode på opp mot 100 år.
Men et annet estimat av underliggende trend ville endret dette.
Så en sikker konklusjon om at det er sykler i HadCrut dataene kan ikke trekkes fra denne analysen.
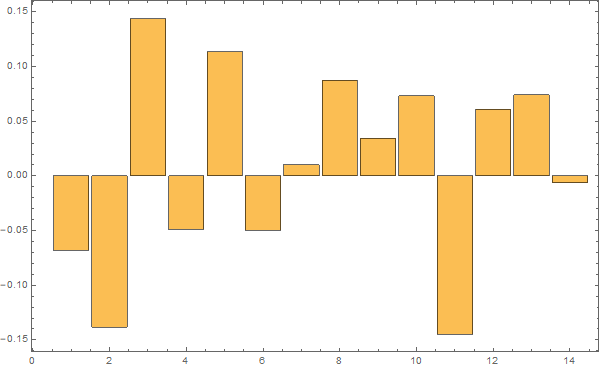
Tillegg: For ordens skyld, 10 tilfeldige realisasjoner.
![]() ,
, ![]() og
og ![]() om forskyvningen til de to O-atomene og C-atomet i forhold til likevektsposisjonen.
om forskyvningen til de to O-atomene og C-atomet i forhold til likevektsposisjonen.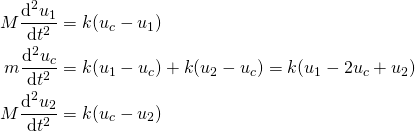
![]()
![]() ,
, ![]() og
og ![]() er i prinsipp komplekse tall, for å ta hånd om eventuelle faseforskjeller mellom de tre atomene.
er i prinsipp komplekse tall, for å ta hånd om eventuelle faseforskjeller mellom de tre atomene.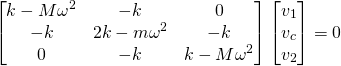
![]() , med løsninger
, med løsninger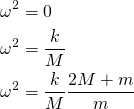
![]() er funnet, kan vi sette den tilbake inn i matriselikningen og finne
er funnet, kan vi sette den tilbake inn i matriselikningen og finne ![]() ,
, ![]() , og
, og ![]() . Det gir
. Det gir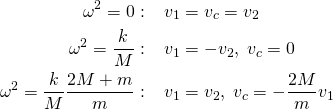
![]()
![]()