Når økende CO2-nivå i atmosfæren øker temperaturen, avtar havets evne til å løse CO2. Det betyr at det er en positiv tilbakekopling: CO2 øker pga våre utslipp, og øker så litt til pga temperatureffekten i havet.
Hos Klimarealistene reiser signaturen Jan Rune dette spørsmålet 4. juni 2018, og ser ut til å konkludere med at CO2-nivået vil «gå bananas».
Et «metasvar» på dette er at om Jan Runes konklusjon var korrekt, ville det vært velkjent og innarbeidet i klimamodellene.
Men det kan være greit å avklare det også med enkle faglige argumenter, for spørsmålet er relevant.
Hos Klimarealistene kom det hurtig en «bla, bla» kommentar, men da det etter en uke ikke var kommet noe seriøst, la jeg inn en kommentar:
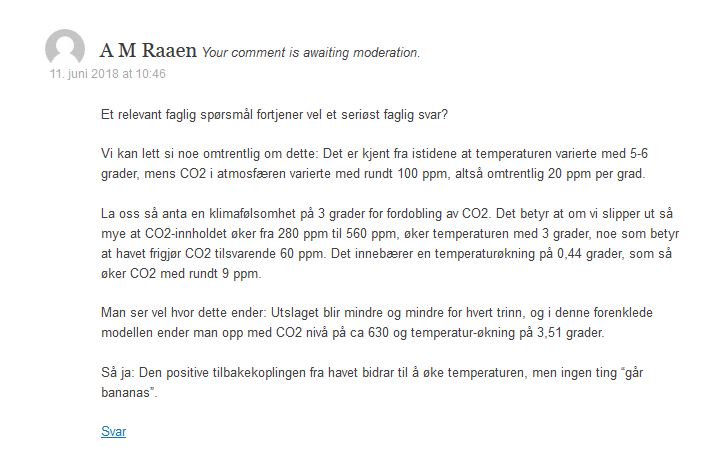
Tallene var basert på enkle beregninger i et regneark – noe alle med ørlite erfaring med regneark lett kunne gjort.
Etter noen timer var det borte. Redaktøren hadde tilsynelatende bestemt at «Klimarealister» må skånes for enkel fysikk.
Dette måtte da være et uhell? Så jeg repostet det samme. Og det forsvant enda fortere. Faglige resultater man ikke liker blir altså slettet. Klimarealistene sensurerer.
Analytisk tilnærming
For slike enkle problemstillinger er regneark kjapt og enkelt, men her kommer man også langt analytisk:
For forståelsens del starter vi først med en forenklet modell: Temperaturen øker lineært med CO2 nivået.
Vi starter med en situasjon hvor CO2 nivået hurtig øker fra 260 til 560 ppm, og antar at det gir en økning i temperaturen på 3 grader.
Det betyr at vi kan skrive:
![]() (*)
(*)
der ![]() er CO2-konsentrasjonen i ppm. Med antagelsene over blir da
er CO2-konsentrasjonen i ppm. Med antagelsene over blir da
![]() grad per ppm
grad per ppm
Vi antar så at én grad temperaturøkning fører til utgassing av 20 ppm CO2.
Det skriver vi som
![]()
der ![]() ppm/grad.
ppm/grad.
Situasjonen er altså som følger: Vi øker først CO2-nivået fra 280 til 560 ppm, som vi benevner ![]() . Det fører til en temperaturøkning gitt av
. Det fører til en temperaturøkning gitt av
![]()
og dermed en resulterende CO2 økning fra utgassing av havet gitt av
![]()
Her kan vi eliminere ![]() og får dermed
og får dermed
![]()
Men denne økte konsentrasjon har en temperatur-effekt, og påfølgende utgassing, som igjen har en temperatureffekt, osv. Man ser at totaleffekten blir
![]()
Man kjenner igjen en geometrisk rekke, som man vet konvergerer om ![]() :
:
Man ser altså at i denne enkle modellen går CO2-nivået «bananas» om ![]() (som er langt over den reelle verdien.)
(som er langt over den reelle verdien.)
Men temperaturen er ikke lineær i CO2-nivået – den er logaritmisk – en svakere økning.
Likningen merket med (*) blir da:
![]()
der vi nå har ![]()
Vi ser at hvert trinn, som i modellen over ga en faktor ![]() nå gir
nå gir ![]() . Vi har ikke lenger en geometrisk rekke.
. Vi har ikke lenger en geometrisk rekke.
Vi ser at
![]()
der ulikheten kommer fra egenskapene til logaritmefunksjonen.
Det betyr at økningen ved hvert trinn er mindre enn
![]()
Man ser at faktoren fra den forrige modellen skal deles med den stadig økende konsentrasjon. Det betyr at uansett hvilke verdier av ![]() og
og ![]() man starter med, vil man etter noen trinn ende opp med en faktor som er mindre enn 1: Det kan aldri bli ustabilitet i denne modellen.
man starter med, vil man etter noen trinn ende opp med en faktor som er mindre enn 1: Det kan aldri bli ustabilitet i denne modellen.
Konklusjonen er enkel å reprodusere i et regneark: I den linære modellen finner man ustabilitet som forventet, mens i den logaritmiske finner man ikke ustabilitet uansett parametre.
Arne Marius Raaen
