Den symmetriske og den asymmetriske strekkmoden innebærer begge vibrasjon langs molekylets akse (se Drivhusgassen CO2, del 1).
Vibrasjonsfrekvensene bestemmes av stivhetene til de to bindingene, som må være like, og massene til atomene.
Man vil da forvente at det må være en sammenheng mellom frekvensene til de to modene, og skal her se på hva en klassisk beskrivelse sier om det.
La oss kalle stivheten for k, massen til O for M, og massen til C for m. La oss videre skrive ![]() ,
, ![]() og
og ![]() om forskyvningen til de to O-atomene og C-atomet i forhold til likevektsposisjonen.
om forskyvningen til de to O-atomene og C-atomet i forhold til likevektsposisjonen.
Newtons 2. lov gir da 3 likninger:
(1) 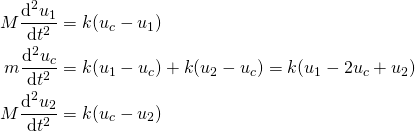
Vi er interessert i løsninger som vibrerer harmonisk, så vi antar derfor at vi har
(2) ![]()
og tilsvarende for de to andre. ![]() ,
, ![]() og
og ![]() er i prinsipp komplekse tall, for å ta hånd om eventuelle faseforskjeller mellom de tre atomene.
er i prinsipp komplekse tall, for å ta hånd om eventuelle faseforskjeller mellom de tre atomene.
Når vi setter inn i likningene over, får vi et resultat som kan skrives som en matrise-likning:
(3) 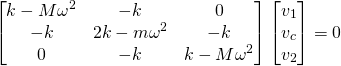
Dette er et homogent likningssett, hvor kravet til at det skal finnes løsninger er at determinanten til matrisen er null – matrisen må være singulær.
Dette gir en tredjegradslikning i ![]() , med løsninger
, med løsninger
(4) 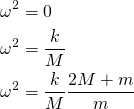
Når ![]() er funnet, kan vi sette den tilbake inn i matriselikningen og finne
er funnet, kan vi sette den tilbake inn i matriselikningen og finne ![]() ,
, ![]() , og
, og ![]() . Det gir
. Det gir
(5) 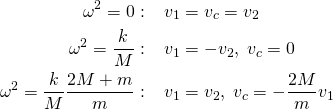
Den første er homogen translasjon av molekylet uten vibrasjon, den andre er den symmetriske strekkmoden og den tredje er den asymmetriske strekkmoden.
Vi ser at forholdet mellom frekvensene til asymmetrisk og symmetrisk strekk er
(6) ![]()
Med den asymmetriske moden på 2349 cm-1 (se Figur 3 i Del3) blir da prediksjonen for den symmetriske moden 1227 cm-1.
Til sist kan man merke seg at for asymmetrisk strekk har man
(7) ![]()
som viser at den asymmetriske moden ikke har total bevegelsesmengde, slik det må være.
Man ser ikke den symmetriske moden direkte i infrarød spektroskopi, men som vi så i Figur 8 i Del 1 ser man den indirekte. Ut fra dette kan man estimere forventede frekvenser:
667 cm-1 + 618 cm-1= 1285 cm-1 og 667 cm-1 + 720 cm-1 = 1387 cm-1 der 667 cm-1 er senterfrekvens til bøyemoden.
I Raman spektroskopi forventer man altså topper rundt 1285 cm-1 og 1387 cm-1 for CO2
