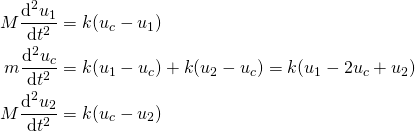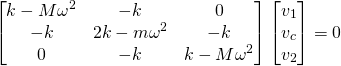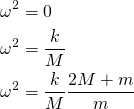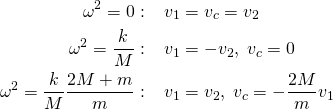Virrevandring | Sporadiske og usystematiske drypp om klima og annet

Stabilitet av statisk atmosfære

Skrevet 6. desember 2025 av A M Raaen

Drivhuseffekten har med jordas energibalanse å gjøre. Når konsentrasjonen av drivhusgasser øker, vil høyden som energien i gjennomsnitt stråler ut fra øke. Hva som skjer ved jordoverflaten avhenger da av temperatur-profilen i atmosfæren.

Det er velkjent at temperaturen avtar med høyden. Derfor, når utstrålingshøyden øker blir overflaten varmere.

Det er fascinerende at temperatur-profilen i atmosfæren i grove trekk bestemmes av svært enkle argumenter, basert på stabiliteten til en statisk atmosfære.

Kraftlikevekten

Det fundamentale kravet for stabiliteten til atmosfæren er at hvis man ser på et lite volumelement, må forskjellen mellom trykk-kraft nedenfra og trykk-kraft ovenfra akkurat være nok til å bære tyngden av dette volumelementet. Sagt på en annen måte, trykket på en gitt høyde er akkurat stort nok til å bære vekten av overliggende atmosfære.

Stabilitet

Men at kraftlikevekt er oppfylt er ikke et tilstrekkelig kriterium: likevekten må være stabil.

Dette er illustert i et enkelt mekanisk system i figuren under. For begge de to kulene er kraftlikevekt oppfyllt, men de oppfører seg vidt forskjellig om det kommer en liten forstyrrelse. Den røde til venstre finner tilbake til sin posisjon, mens den blå til høyre forsvinner. Til venstre er likevekten stabil, til høyre er likevekten ustabil.

For atmosfæren er tilsvarende spørsmål hva som skjer om et lite element av luft beveger seg oppover. Hvis det får mindre tetthet enn omgivelsene på den nye høyden, vil det fortsette videre: Likevekten er ustabil. Får det større tetthet enn omgivelsene på den nye høyden, vil det bevege seg ned til utgangspunktet: Likevekten er stabil.

Når man analyserer situasjonen, finner man at en tørr atmosfære vil være stabil om temperaturen faller med 9,8 grader eller mindre per kilometer. Faller den mer enn 9,8 grader per kilometer er atmosfæren ustabil.

Dette betyr om det er «noe» som avkjøler atmofæren slik at temperaturen faller mer enn 9,8 grader per kilometer, vil atmosfæren bli ustabil, og søke mot 9,8 grader per kilometer. Dette betyr at for en tørr atmosfære vil en svært ofte observere omtrent 9,8 grader per kilometer. For en fuktig atmosfære er tallet noe lavere.

Dette «noe» som tillater atmosfæren å kvitte seg med energi er drivhusgassene (og skyene). Drivhusgassene er derfor sterkt medskyldig i at atmosfæren over alt har omtrent samme temperaturutvikling med høyde (med en korreksjon for fuktighet).

Noen likninger – litt termodynamikk

Jeg viser nå hvordan konklusjonen over støttes av fundamentale termodynamiske likninger.

Utgangspunktet er kraftlikevekten, som kan skrives

(1) $\begin{equation*} \frac{d p}{d z}= -\rho g \end{equation*}$

Her er $p$ trykket, $\rho$ tettheten og $g$ tyngdens akserelasjon. Vi lar $z$ -aksen peke oppover. Vi bruker så den ideelle gassloven

(2) $\begin{equation*} p V = n R T \end{equation*}$

Ved å bruke molvekten $M$ kan vi skrive dette som

(3) $\begin{equation*} p = \frac{M n}{V} R T \frac{1}{M}= \rho \frac{R}{M}T \end{equation*}$

Med dette kan vi eliminere $\rho$ i (1), og får

(4) $\begin{equation*} \frac{d p}{d z}= -p \frac{M g}{R}\frac{1}{T} \end{equation*}$

For å forenkle litt, antar vi nå at temperaturen avtar (eller stiger om $\alpha$ er negativ) lineært med høyden:

(5) $\begin{equation*} T = T_0 -\alpha z \end{equation*}$

Da blir (4)

(6) $\begin{equation*} \frac{dp}{p}= -\frac{M g}{R}\frac{1}{T_0-\alpha z} dz \end{equation*}$

som integreres til

(7) $\begin{equation*} \ln\frac{p}{p_0}= \frac{M g}{R\alpha}\ln\frac{T_0-\alpha z}{T_0} \end{equation*}$

og dermed

(8) $\begin{equation*} p=p_0 \left(1-\frac{\alpha z}{T_0}\right)^\frac{Mg}{R\alpha} \end{equation*}$

Vi kan nå bruke (3) til å introdusere tettheten:

(9) $\begin{equation*} \rho \frac{R}{M}(T_0-\alpha z)=\rho_0 \frac{R}{M}T_0 \left(1-\frac{\alpha z}{T_0}\right)^\frac{Mg}{R\alpha} \end{equation*}$

og dermed

(10) $\begin{equation*} \rho=\rho_0 \left(1-\frac{\alpha z}{T_0}\right)^{\frac{Mg}{R\alpha}-1} \end{equation*}$

Vi trenger å vite hvordan denne funksjonen endrer seg rundt en gitt høyde $z$ . Vi kan derivere direkte, men kommer litt enklere til målet ved å ta logaritmen på begge sider først

(11) $\begin{equation*} \ln \rho=\ln \rho_0 + (\frac{Mg}{R\alpha}-1) \ln(1-\frac{\alpha z}{T_0}) \end{equation*}$

Derivering:

(12) $\begin{equation*} \frac{\rho'}{\rho}=(\frac{Mg}{R\alpha}-1) \frac{-\frac{\alpha}{T_0}}{1-\frac{\alpha z}{T_0}}=-(\frac{Mg}{R\alpha}-1)\frac{\alpha}{T} \end{equation*}$

Altså

(13) $\begin{equation*} \rho'=-\rho (\frac{Mg}{R\alpha}-1)\frac{\alpha}{T}=-\rho (\frac{Mg}{R}-\alpha)\frac{1}{T} \end{equation*}$

Dette viser altså hvordan tettheten avtar oppover i henhold til kraftlikevekten. Alle $\alpha$ , positive og negative, oppfyller likevekten. Kraftlikevekt alene kan ikke bestemme $\alpha$ .

Neste trinn er å sjekke stabiliteten.

Adiabatisk volumforandring

Når et lite luftelement beveger seg, er det en god antagelse å anta at det ikke utveksler varme med omgivelsene. Dette kalles en adiabatisk prosess, og da gjelder følgende relasjon mellom tetthet og trykk:

(14) $\begin{equation*} \frac{p}{\rho^\gamma}=\mathrm{const} \end{equation*}$

$\gamma$ er den adiabatiske konstant. Vi må finne ut hvordan dette uttrykket endrer seg ved en gitt $z$ . Igjen er det nyttig å ta logaritmen før derivering:

(15) $\begin{equation*} \ln p -\gamma \ln\rho=\ln(\mathrm{const}) \end{equation*}$

Ved derivasjon

(16) $\begin{equation*} \frac{p'}{p}-\gamma \frac{\rho'}{\rho}=0 \end{equation*}$

Vi ordner litt, og setter inn for $p'$ fra likning (1)

(17) $\begin{equation*} \frac{\rho'}{\rho}= \frac{1}{\gamma}\frac{p'}{p}=-\frac{1}{\gamma}\frac{\rho g}{p} \end{equation*}$

På høyre siden kan vi eliminere $p$ og $\rho$ med ideell gass likningen (3)

(18) $\begin{equation*} \frac{\rho'}{\rho}= \frac{1}{\gamma}\frac{p'}{p}=-\frac{1}{\gamma}g\frac{M}{R T} \end{equation*}$

Altså

(19) $\begin{equation*} \rho'=-\rho\frac{Mg}{\gamma R T} \end{equation*}$

Vi har nå to likninger (13) og (19) for den deriverte av tettheten $\rho$ . Den første viser hva kraftlikevekten krever, den andre viser hva som vil skje med et lite element som beveger seg oppover. Fra innledningen husker vi at atmofæren er stabil om det lille elementet som har beveget seg oppover har større tetthet en omgivelsene, altså at tettheten må ha endret seg mindre enn det kraftlikevekten krever. Kravet for stabilitet blir da

(20) $\begin{equation*} \frac{M g}{\gamma R T} < \frac{M g}{RT}-\frac{\alpha}{T} \end{equation*}$

som betyr

(21) $\begin{equation*} \alpha < \frac{Mg}{R}-\frac{M g}{\gamma R}=\frac{Mg}{R}\left(1-\frac{1}{\gamma}\right)=\frac{Mg}{R}\frac{\gamma -1}{\gamma} \end{equation*}$

Tallverdi

Vi kan nå sette inn tallverdier. For luft er molvekten nær 29 gram per mol, tyngdens akserelasjon er omtrent 9,8 m/ $\mathrm{s}^2$ , den universelle gasskonstanten er omtrent 8,3 J/(K mol), og for en 2-atomig gass, som dominerer atmosfæren, er $\gamma$ nær 1,4.

Vi får da stabilitetskriteriet som

(22) $\begin{equation*} \alpha < 9,8\, \mathrm{K}/\mathrm{km} \end{equation*}$

Dette stemmer med noe alle fjellvandrere vet: Temperaturen faller typisk med 1 grad per 100 meter. Den enkle, statiske utledningen over er derfor hovedmekanismen som bestemmer den storskala temperatur-profilen i atmosfæren. Det er derfor man ofte ser temperaturen mot høyde omtalt som «adiabaten».

Forbehold

Utledningen har gjentatte ganger brukt den ideelle gassloven. For atmosfærisk trykk er det en svært god tilnærmelse til oppførselen til de fleste gassene, men det er et viktig unntak: vanndampen.

Årsaken er at luften bare kan ha en viss andel vanndamp, og denne andelen blir mindre når det blir kaldere. Når fuktig luft stiger vil den derfor kondensere til vann, og fordampningsvarmen frigjøres. Det bidrar til å varme opp atmosfæren, slik at temperaturen faller noe mindre med høyden, «den fuktige adiabat».

Drivhusgassenes rolle

For at statisk stabilitet skal gi en så nær universal temperaturstruktur i atmosfæren, er det en fundamental forutsetning: Drivhusgassene må avkjøle atmosfæren så mye at ustabiliteten (konveksjonen) starter.

For de nederste omtrent 10 km av atmosfæren, troposfæren, gjelder følgende med god tilnærmelse:

Solen varmer overflaten, som varmer atmosfæren nedenfra. Drivhusgassene bidrar til at troposfæren kvitter seg med energi, gradienten blir så høy at konveksjonen drives, og en nær universell temperatur-struktur oppstår (9,8 grader per km i tørre forhold, en del mindre i fuktige forhold.)

Når vi slipper mer drivhusgasser inn i atmosfæren, vil det ikke påvirke temperatur-gradienten: Det er allerede nok drivhusgasser til å gi nok kjøling til at konveksjonen drives. Men mer drivhusgasser betyr en atmosfære som er tettere for stråling, og strålingen som unnslipper til verdensrommet og styrer planetens energibalanse må starte lenger oppe. Det betyr flere høydemetere for konveksjonen å virke på, og større forskjell mellom temperaturen ved den midlere utstrålingshøyden og overflaten.

Ingen som har forstått denne sammenhengen, kan være det minste i tvil om at økt innhold av drivhusgasser er en driver for økt temperatur. Det er ikke et tvilsspørsmål.

Hvor mye avhenger imidlertid f.eks. av hva som skjer med skyene, og mange andre mekanismer. Det er et komplisert spørsmål som denne enkle analysen ikke kan besvare.

Den enkle, robuste fysikken sammen med temperaturutviklingen, spesielt de siste 50 år, etterlater lite tvil. Når aldrende politikere likevel stiller spørsmål om CO2’s effekt framstår det kun som ideologi. Totalt uansvarlig ideologi. Jeg minner om hva nobelprisvinner i fysikk Steven Weinberg skrev: «It is generally foolish to bet against the judgements of science, and in this case, where the planet is at stake, it is insane.»

Stratosfæren

Går man til neste lag i atmosfæren, stratosfæren, er omstendighetene andre. Her bidrar osons absorpsjon av ultrafiolett solstråling til en ekstra varmekilde. Temperaturen øker med høyden, og konveksjon stopper opp. («Strato» kommer fra gammelt gresk og betyr noe sånt som lagdelt.) Det er derfor mye mindre vertikal miksing i stratosfæren enn i troposfæren.

Sluttbemerkning

Jeg har prøvd å gjøre presentasjonen av likningene så lett tilgjengelig som mulig ved å ta med mange mellomtrinn. De som fulgte godt med i fysikk- og matematikk-timene på videregående burde kunne følge argumentasjonen.

Mangler man bakgrunn i fysikk og matematikk fra videregående, er det nok krevende å forstå hva som skjer.

Det er fullt mulig å tenke seg at ideologer som uttaler seg om CO2’s effekt kan ha problemer med likningene.

I så fall vil jeg presisere at det jeg har presentert er aldeles elementært, og legger nok beslag på bare en del av en av de aller første forelesningene i et grunnkurs i fluidmekanikk. Det er svært langt opp før man kan lese og forstå mye av publikasjonene i klimavitenskapen.

Ettertanke

Man vil observere at vi antok en lineær utvikling av temperatur med høyden, og endte opp med en lineær utvkling av temperaturen med høyden. Er argumentet sirkulært?

Men: Det var bare i første del vi gjorde denne antagelsen. Kraftlikevekten i seg selv kan ikke bestemme temperatur-gradienten.

I andre del, der vi lot den adiabatiske lov styre, gjorde vi ingen a priori antagelse om temperaturen, og endte opp med en temperatur som faller lineært med høyden.

Jeg valgte å beregne tettheten i begge tilfellene, fordi sammenlikning av tetthetene umiddelbart knytter forbindelsen til atmosfærens stabilitet. Drivhusgassenes nødvendige rolle for å gi et utgangspunkt for konveksjonen blir aldeles åpenbar. Til sammen forklarer dette hvorfor atmosfæren under normale forhold ender opp med den adiabatiske temperaturgradienten, 9,8 grader per kilometer i tørr atmosfære.

Vi kan lett gå direkte fra likning (19) for tettheten til en likning for temperaturen. Vi tar utgangspunkt i den adiabatiske likningen (14), og bruker den ideelle gassloven (2) til å eliminere $p$ .

Da finner vi

(23) $\begin{equation*} \rho \,T^\frac{1}{1-\gamma}=\mathrm{const} \end{equation*}$

Vi tar som før logaritmen

(24) $\begin{equation*} \ln{\rho}+\frac{1}{1-\gamma}}\ln T=\ln(\mathrm{const}) \end{equation*}$

og deriverer

(25) $\begin{equation*} \frac{\rho'}{\rho} + \frac{1}{1-\gamma}\frac{T'}{T} = 0 \end{equation*}$

Dermed har vi ved hjelp av (19)

(26) $\begin{equation*} T' =T (1-\gamma)\frac{\rho'}{\rho}=T (1-\gamma)\frac{Mg}{\gamma R T}=-\frac{Mg}{R}\frac{\gamma-1}{\gamma} \end{equation*}$

Ved å anta at trykket følger likevektslikningen (det må det!) og at sammenhengen mellom trykk og temperatur er gitt av den adiabatiske lov, har vi altså funnet at stigningstallet til temperaturen er konstant over troposfærens høyde, og lik et temperaturfall på 9,8 grader per kilometer under tørre forhold.

Utledningen i dette avsnittet er mer kompakt, men gir ikke på samme måte innsikt i hvorfor atmosfæren beveger seg mot «adiabaten» – for det trenger vi stabilitetsanalysen.

Kilder

Ideen til presentasjonen her er hentet fra et gammelt notat fra forelesninger i et innføringskurs i fluidmekanikk, gitt av (senere) professor Tor Ytrehus i 1975. Jeg har prøvd å forenkle mest mulig, og tatt med mer mellomregninger. Jeg har også brukt Hemmers Termisk fysikk, se side 32-33. All argumentasjon rundt drivhusgasser er min egen – de var mindre framme i 1975.

Sitatet fra Weinberg er fra kapittel 20 i hans bok «Third thoughts» fra 2018. Setningen ble opprinnelig uttalt 16. juni 2017, da Weinberg var en av 4 som ble æresdoktor ved Rockefeller University.

Skrevet i Ukategorisert | Legg igjen en kommentar

Ole Østlid, Værstat og vintertemperaturen i Norge

Skrevet 10. november 2025 av A M Raaen

Værstat hadde 3/11-2025 et innlegg med tittel NRK tilbakeholder vesentlig informasjon om utviklingen i norske vintre.

Her er noen sitater fra artikkelen:

«Ingen signifikant trend i norske vintertemperaturer i perioden 1900-2020»
«Det NRK gjør i denne saken er å se bort fra funnene i rapporten, og kun fokusere på økningen i vintertemperaturene fra den kjølige perioden på 1980-tallet.»
«NRK nekter å informere om forskningsfunnene om utviklingen i norske vintertemperaturer.»
«NRK vil ikke gi en kommentar på hvorfor de mener de ikke trenger å opplyse om forskningsfunnene som har sigifikanstestet utviklingen i vintertemperaturer i Norge.»

Det går an å tenke at Østlig mener at NRK, kanskje til og med bevisst, feilinformerer om klimautviklingen.

La oss se litt nærmere på dataene for å ettergå dette.

Datagrunnlaget er lett tilgjengelig

Man går bare inn på nettstedet Se Klima

Så velger man etter tur:

«Sesonger»
«Regionmiddeltemperatur, avvik fra normalen 1991–2020 (årstid)»
«Alle år»
«Region Norge»

og kan laste ned et excelark med data. Fra det må man plukke ut vintersesongen, og så kan man analysere den.

Dataanalyse

Dataene fra 1920 til 2020 ser slik ut, der den røde linjen er beste tilpasning til en rett linje.

Den røde linjen stiger knapt en grad på 120 år (0,081 grader per år), mens temperaturen ofte hopper 4–5 grader fra ett år til det neste. Det er åpenbart at det er atskillig usikkerhet knyttet til hvor stort stigningstallet egentlig er.

Usikkerheten kan kvantifiseres med den såkalte P-verdien som statistikkprogrammer beregner. Den kan sees på som sannsynligheten for at man kan få den rød linjen om det egentlig ikke er noen trend i dataene. For disse dataene er P = 0,11, altså det er 11 % sjanse for at data uten trend (men med samme spredning) kan gi den røde linjen. I statistikk legger man ofte grensen på hva som er statistisk signifikant på 5 %, så trenden i dette datasettet blir dermed karakterisert som ikke statistisk signifikant.

Men et poeng er viktig her: man kan beregne P-verdi for en vilkårlig stigning, ikke bare for null. F.eks. er det også 11 % sjanse for at data med en underliggende stigning på 0,162 grader per år kan gi en observert stigning på 0,081.

Når Værstat fokuserer bare på tilfellet uten signifikant stigning, underslås dette poenget fullstendig. Skal man framheve 0-tilfellet over 0,016 tilfellet, trengs det en argumentasjon! Værstat har ingen.

Nullhypotesen

I statistikk har dette sammenheng med valget av «Nullhypotese». Man har en forståelse av problemstilligen som gjør at man kan formulere det man tror er mest sannsynlig, og så sjekker man om denne hypotesen er konsistent med dataene.

Man kan si at Værstat har valgt null trend som sin nullhypotese. Dataene tilsier at denne hypotesen ikke kan forkastes! Men det betyr ikke at hypotesen om null trend er bekreftet. Det er stor forskjell på å «ikke kunne forkaste» og å «bekrefte«. For som vi har sett, en hypotese om 0,016 grader per år kan heller ikke forkastes.

Er så null trend en rimelig nullhypotese? Det er den nok ikke, for vi vet at temperaturen i verden er økende, vi vet at de fleste sesonger har statistisk signifikant økning i Norge siden 1900. Vi har til og med en forståelse for hvorfor temperaturen er økende – drivhusgassene! En nullhypotese som innebærer økning av vintertemperaturen er mye mer naturlig.

Statistisk analyse viser at det er 95 % sjanse for at stigningstallet til datasettet er mellom -0,0018 og 0,018 grader per år. Null stigning – som Værstat fokuserte så mye på – er helt i ytterkant av dette området.

Man kan merke seg at om man tar med data fram til og med 2023 (bare 3 år mer!), blir intervallet -0,00085 til 0,018. Det er nærliggende å tro at om svært få år blir trenden statistisk signifikant økende.

Konklusjon

Værstat kom med noen heftige uttalelser om NRK. De synes å være basert på en betydelig overfortolkning av hva som ligger i at trenden ikke er statistisk signifikant. Med en dypere analyse framstår NRK’s artikkel som rimelig saklig og balansert. Konklusjonen er at Værstat burde dempet tonen atskillig!!

Skrevet i Ukategorisert | Legg igjen en kommentar

Enda mer om Professor Olav Martin Kvalheim, Klimarealistene, AMO, og havnivået i Bergen

Skrevet 31. oktober 2025 av A M Raaen

Jeg har i et par innlegg vist at det ikke er grunnlag for Kvalheims konklusjon om at havnivået ikke utgjør noen risiko i Bergen, og heller ikke for hans påstand om at det er dominert av AMO – Atlantic Multidecadal Oscillasjon.

Nå har Kvalheim gjentatt sine påstander i Nettavisen. [Kvalheim benevner en gang i innlegget AMO for NAO, som er et helt annet atlantisk værfenomen. Det er en trykkfeil.]

På denne bakgrunn er det på sin plass å presisere hvor aldeles elementært mitt argument var: Jeg korrigerte den observerte endringen med den godt kjente landhevingen, og fikk en kurve som så slik ut:

Det er helt åpenbart at en 60–70 års syklus ikke kan forklare denne oppførselen. Og det synes klart ut at økningen har blir raskere i det siste. Dataene gir dermed ikke grunnlag for å avvise stigning i Bergen.

Man må undres på at en professor i naturvitenskap ikke gjør enkle undersøkelser før han drar såpass bastante konklusjoner.

Er det spor av AMO?

Man kan selvsagt ikke utelukke at det er en liten signatur fra AMO i dataene. La oss gjøre et litt mer rigorøst forsøk enn professor Kvalheim på å kvantifisere den!

Jeg vil gjøre dette ved trinnvis å tilpasse en konstant funksjon, en lineær funksjon, en kvadratisk funksjon og en kontinuerlig bilineær funksjon til dataene.

For hvert tilfelle viser jeg to plot. Ett viser dataene korrigert for landhevning sammen med den tilpassede modellen. Det andre viser avviket mellom dataene og den tilpassede modellen. På dette plottet vises et rødt tall som er summen av kvadratisk avvik mellom data og modell.

Konstant tilpasning

Den røde linjen svarer her til middelverdien av dataene. Denne tilpasningen er ikke særlig interesseant, fordi den beskriver dataene såpass dårlig, men jeg har den med for å illustrere utviklingen i avvikene mellom modellen og dataene etter hvert som modellen forbedres. Summen av avvikene kvadrert er her nesten 400000.

Lineær tilpasning

Neste trinn er tilpasning av en rett linje. Som man ser reduseres avvikene atskillig, summen av kvadratene er nå knapt 130000. Men man ser at det forsatt er en struktur i avvikene, de er gjennomgående positive tidlig og sent, og gjennomgående negative på midten.

Kvadratisk

Kvadratisk tilpasning reduserer avvikene ytterligere, summen av kvadratiske avvik er 108000. Man kan ikke lenger se tydelig at det er en struktur i avvikene. Modellen pluker med andre opp den langsiktige utviklingen ganske bra.

Kontinuerlig bilineær tilpasning

Den bilineære tilpasning gjør en litt bedre jobb enn den kvadratiske, summen av kvadrerte avvik er nå knapt 101000. Man ser ingen klar langsiktig struktur i avvikene.

Syklisk tilpasning, 65 år periode, til residuene fra bilinært

Både kvadratisk og bilineær tilpasning fjerner den åpenbare stigningen i dataene. Vi kan derfor undersøke om det er igjen en rest av en syklus på 60–70 år i avvikene. Vi bruker modellen over med best tilpasning, den bilinære, og prøver å tilpasse en 65 år syklus til avvikene fra den.

En syklisk funksjon kan skrives slik:

(1) $\begin{equation*} f(t)=b + a\left (1-\cos(\frac{2\pi}{T}(t-t_0))\right ) \end{equation*}$

Man ser at denne funksjonen har middelverdi $b$ , og den har ett bunnpunkt (for positiv $a$ ) eller toppunkt (for negativ $a$ ) ved $t = t_0$ .

Funksjonen er ikke-linær i parameterne $T$ og $t_0$ . Det betyr at man må bruke en ikke-linær metode for å bestemme dem. En viktig karakteristikk ved en ikke-linær metode er at den ikke nødvendigvis finner den aller beste løsnignen, den kan konvergere mot et «lokalt optimum». Dette kan man sjekke ved å gi modellen forskjellige startpunkter og se om svaret blir det samme.

Figurene viser hva man får når man holder $T$ fast på 65 år, men lar de øvrige parameterne være fri. Ulike startverdier for $t_0$ ser ut til å gi samme resultat, og summen av kvadratisk avvik er litt redusert. Alt i alt er det svak indikasjon på en 65-års sykel med amplitude på rundt 7 mm.

Syklisk tilpasning, fri periode, til residuene fra bilineær

Dette er som tilfellet over, men man lar algoritmen bestemme også perioden. Det gir en litt lengre periode, ca 85 år, med ørlite bedre tilpasning. Amplituden er øket til 8,5 mm.

Alt i alt åpner dataene for en usikker konklusjon om at det er et AMO signal i dataene, men det utgjør godt under 10 % av hele utslaget.

Tilpasning av syklisk oppførsel til de landheving-korrigerte dataene.

Jeg slo uten videre fast at det er åpenbart at en 60–70 års syklus ikke kan forklare oppførselen i den første figuren. La oss for ordens skyld prøve på en tilpasning.

Hvis vi låser perioden til 65 år får vi de neste to figurene. En ser at tilpasningen er svært dårlig, summen av kvadratisk avvik er bare litt mindre enn for den rette linjen.

Kanskje går det bedre for en lengre periode? La oss prøve 200 år. Tilpasningen er blitt atskillig bedre, den er omtrent som for den rette linjen.

Her kan man bli fristet til å forsøke å la algoritmen bestemme også perioden, men før man gjør det bør man analysere litt: Når perioden blir lang i forhold til observasjonsperioden kan man rekkeutvikle funksjonen $f(t)$ og bare ta med det dominerende leddet:

(2) $\begin{equation*} f(t)=b + 2\pi^2 \frac{a}{p^2}\left(t-t_0 \right)^2 \end{equation*}$

Vi har fått en kvadratisk funksjon, og $a$ og $p$ inngår på samme plass. Det betyr at det er umulig for algoritmen å bestemme $a$ og $p$ entydig om vi lar begge være frie. Men vi ser at vi forventer at når perioden er lang nok, vil den sykliske tilpasningen gjenskape den kvadratiske! Figuren under viser tilfellet for periode 5000 år. Vi ser at summen av de kvadratiske avvikene er bare ubetydelig større enn for det kvadratiske tilfellet lenger oppe (108474 mot 108455).

Vi kan ikke på noen meningsfull måte tilpasse en syklisk funksjon til dataene. Professor Kvalheim villeder sine lesere!

For ordens skyld:

Det er ingen ting i analysen jeg gjør som kan verifisere eller falsifisere seriøse prediksjoner av havnivå. Til det er den alt for banal. Men den kan falsifisere Kvalheims lettvinte påstander om at økning i havnivå ikke er en trussel.

For den som har lyst til å høre en seriøs havnivåforsker: Bruk litt tid på f.eks. denne.

Skrevet i Ukategorisert | Legg igjen en kommentar

Mer om Professor Olav Martin Kvalheim, Klimarealistene og havnivået i Bergen

Skrevet 22. oktober 2025 av A M Raaen

Den 25 april publiserte jeg et innlegg om Kvalheim og havnivået i Bergen, der jeg klart konkluderte med at hans argumentasjon ikke holder mål.

Kvalheim kommenterte dette hos Klimarealistene 17/10. Hans argumentasjon var i stor grad en gedigen stråmann, noe jeg kommenterte. Kvalheims svar på dette unngikk kritikkens substans, men opprettholdt hans påstand om ingen havnivåstigning forventet i Bergen.

I tillegg satte han fram en konkret påstand:

«Mellom disse to periodene faller det relative havnivået noen cm før det igjen går oppover. Dette skyldes en syklisk naturlig variasjon kjent som den Atlantiske multi-dekale oskillasjonen (AMO). Den har en periodisitet på 60-70 år slik jeg nevnte i mitt forrige svar. AMO opptrer som en svingning rundt regresjonslinjen med maksimalt utslag på noen cm.«

La oss se litt nærmere på denne påstanden.

For det første kan vi si med sikkerhet at landhevingen ikke følger AMO. Siden landhevingen er sammenliknbar i størrelse med havnivåendringen, bør man korrigere for den før analysen. Kartverket oppgir netto landheving i Bergen til 1,5 cm per år. Hvis vi legger til det, får vi følgende kurve for korrigert havnivåendring:

Men ser umiddelbart at en syklus på 60–70 år umulig kan forklare hovedtrekkene i denne kurven. Om det er en slik syklus til stede i det hele tatt, er den åpenbart minimal!

Videre kan det se ut som noe endrer seg rundt 1980. La oss derfor tilpasse en stykkevis lineær, kontinuerlig funksjon (med 2 segmenter) til dataene. Dette kan vi gjøre med dataene fram til og med 2007, og med alle dataene tilgjengelig.

Dette vises som henholdsvis blå og rød kurve i figuren.

Man kan merke set at der er liten forskjell på den røde og den blå kurven. Med andre ord, det var fullt mulig å dra samme konklusjon allerede i 2008!

Stigningstallet for 2. del av den blå kurven er 28 cm per hundreår, for den røde 30 cm per hundreår

Fra disse tallene må en trekke landhevingen med rundt 15 cm i hundreåret. Man ender derfor opp med atskillig mindre enn det klimaforskerne frykter. Men som Kvalheim riktig poengterte, man kan ikke ekstrapolere en måleserie 75 år fram i tid. Klimaforskernes analyse er da også mye mer komplisert!

Etterord

11 minutter etter at Kvalheim publiserte sin siste kommentar stengte «Redaksjonen» for videre kommentarer. Man kan lure på beveggrunnen. Jeg nøyer meg med å konstatere at Klimarealistene ikke er en papiravis med de begrensninger det setter til spalteplass!

«Redaksjonens» kommentar er spesiell: «.. spåmannen Helge Drange om at havnivået vil stå flere meter over Bryggen i år 2100 om ikke sterke tiltak straks blir satt i gang. De sjamanistiske påstandene til Bjerknessenteret og Drange..«

Dette er usannheter, og usmakelig karakterisering av en fagmann. Det kan synes som at Klimarealistene ikke har noen ambisjoner om en seriøs naturvitenskapelig diskusjon.

Skrevet i Ukategorisert | Legg igjen en kommentar

Ole Østlid, Værstat og havisen

Skrevet 27. august 2025 av A M Raaen

Værstat er et nettsted som retter kritisk blikk på bruk av statistikk i mediene i klimadebatten. Ser man på hvert enkelt innlegg, tenker man at Værstat står for et verdifullt korrektiv, en oppfordring til økt stringens, til det som skrives i media.

Men, tar man ett skritt tilbake og tar et overblikk, får man inntrykk av at Værstat fin-studerer trær, men ikke ser skogen. Følelsen er at alvoret med klimaendringene nesten alltid dysses ned hos Værstat, rett nok bak et ferniss av ryddighet.

—Og det store spørsmålet er: Er Værstat like stringent når fortegnet er motsatt?

Jeg vil diskutere dette ut fra Værstats innlegg om arktisk havis publisert 21/8-2025.
Tittelen er «Forskning bekrefter pause i havisreduksjonen i Arktis»«, og et par utdrag er:

«Dette vil si at forskerne konkluderer med at det ikke er en statistisk signifikant reduksjon i havisnivået i september i Arktis siden 2005.»

«Nesten alle modellene antyder at intern variabilitet i klimaet spiller en viktig rolle i å bremse en menneskeskapte påvirkningen på havisreduksjonen.»

La oss ta utgangspunkt i Værstat’s eget plott av havisen, som inkluderte noen tilpassede rette linjer:

Mitt første spørsmål i slike tilfelle er gjerne: har jeg nok kunnskap til å reprodusere plottet? Som figuren under viser, var svaret denne gangen ja, sa langt man kan se visuelt:

Men det er et vesentlig problem. For å reprodusere Værstats figur måtte jeg gjøre et svært spesielt grep: Årene 1997 og 2007 bidrar både til høyre og venstre. Med andre ord: Disse årene får dobbel vekt i analysen! Det gjør kanskje ikke så stort utslag for 1997, men for 2007 er det rimelig å tro at det er vesentlig. 2007 var et spesielt «uteligger»-år, som altså får bidra dobbelt. Opplagt en juniorfeil, og slett ikke den stringensen Værstat forventer av media.

Slik ser det ut hvis man rydder opp i denne tabben, og lar 1997 og 2007 bidra bare til venstre:

Man ser at den svarte linjen har blitt tydelig brattere!

Det er flere problemer med Værstats analyse: Man ser at linjene krysser hverandre på andre steder enn der dataene skifter farge. Det betyr at det egentlig modelleres sprang i responsen i 1997 og i 2007.

Problemet med det er at når men tilpasser en rett linje, er det en antagelse om at det er et underliggende kontinuerlig forløp, med fluktuasjoner i tillegg. Når man går til flere linjer, er det derfor mest konsistent å bruke en stykkevis lineær, men sammenhengende funksjon for å tilpasse dataene. Er det sprang, bør det begrunnes med helt spesielle forhold akkurat det året, og det har ikke Værstat gjort.

Å tilpasse en stykkevis lineær funksjon er litt vanskeligere enn å tilpasse en rett linje, men det finnes enkel ferdig programvare for det. Figuren under viser resultatet av en slik tilpasning:

Man ser at den venstre linjen er blitt litt slakere, mens den høyre er blitt litt brattere. Den midtre linjen er lite endret.

All kurvetilpasning er beheftet med usikkerhet, men en korrekt analyse kan kvantifisere usikkerheten. Neste figur viser stigningstallene for modellene vi har diskutert, med området for 95% sannsynlighet, dvs at det bare er 5% sannsynlighet for at stigningstallet egentlig er utenfor.

Helt til venstre, i blått, er stigningstallet for en rett linje tilpasset alle datanene. Midlere reduksjon i havisomfang siden 1979 er altså i området 0,6 til 0,9 millioner kvadratmeter per tiår. Det grå området viser dette intervallet i hele plottet.

Det er viktig å påpeke at den anslåtte usikkerheten er basert på en antagelse om at fluktuasjonene er normaltfordelt. Med mange datapunkter er det veldig sannsynlig, men med så korte perioder som 10 år må man forvente avvik. Man bør derfor ikke ta de estimerte usikkerhetene helt bokstavelig.

I rødt ser man de tre stigningstallene for Værstats ufysiske modell, hvor 2007 ble gitt dobbel vekt. Jeg dveler ikke mer med ved den.

I orange er modellen hvor tre uavhengige linjer tilpasses, men hvor 1997 og 2007 bare får lov til å bidra til venstre. Man ser at den høyre linjen går over null, noe som betyr at man ikke kan forkaste en hypotese om at det er null stigning i siste periode. Men man kan også merke seg at det er fullt overlapp mellom de tre symbolene, noe som betyr at man heller ikke kan forkaste en hypotesen om at det er samme stigningstall hele tiden!

(Man kan merke seg at usikkerheten for det midlere området er litt større enn for det røde tilfellet; dette skyldes at det er ett datapunkt mindre i analysen.)

Helt til høyre, i grønt er resultatene for tilpasning av en kontinuerlig, stykkevis lineær funksjon. Vi ser at siden den på en måte tar «alle dataene i en smell» er usikkerheten noe redusert. Det er stort overlapp mellom venstre og høyre intervall, men ikke med det midtre.

Dette betyr at vi ikke kan forkaste en hypotese om at det er samme stigningstall i første og siste del, og det er da nødvendigvis negativt. Vi kan heller ikke forkaste en hypotese om at det er null stigning i siste intervall, siden også det grønne symbolet går opp til over null-streken.

Dette reiser spørsmålet om hva som er den beste nullhypotesen. Og svaret gir seg vel selv, ved at den linære tilpasningen til hele intervallet viser isstap på mer enn 0,6 millioner kvadratkilometer per tiår. Fysikken i problemstillingen er også klar: Den økende CO2-konsentrasjonen i atmosfæren øker klodens middeltemperatur. Det må man forvente vil føre til mindre is over tid. Den naturlige nullhypotesen innebærer derfor at havisen minker med flere hundre tusen kvadratkilometer per tiår, og den kan ikke forkastes ut fra de tilgjengelige dataene.

La oss så se litt nærmere på Værstats utsagn: Det første er hans egen oppsummering i uthevet skrift.

«Dette vil si at forskerne konkluderer med at det ikke er en statistisk signifikant reduksjon i havisnivået i september i Arktis siden 2005.»

Man umiddelbart at her er Værstat er noe upresis, for hva er havisnivå? Det som er diskutert er havisomfang, mens det finns andre forhold som kan undersøkes som sier minst like mye, som havis-volum.

Som vi har sett er det grunnlag for denne påstanden både fra forskningsartikkelen han viser til, og i de analysene jeg har vist. MEN: Når han oppsummerer det i uthevet skrift, har han droppet deler av det fulle bildet. Han har ikke diskutert at en hypotese om konstant reduksjon heller ikke kan forkastes, og ikke gjort noen analyse rundt valg av nullhypotese. Videre har han riktignok nevnt forskningsartikkelens viktige funn at en slik «pause» er fullt mulig/forventet ut fra simuleringer, men han hopper helt over det poenget når kan gir sin egen oppsummerende konklusjon.

Det går an å tenke at Værstat har gjort akkurat det han kritiserer media for, bare med motsatt faglig fortegn. I stedet for å overdrive klimaeffekter, dysses de ned.

Østlids tittel «Forskning bekrefter pause i havisreduksjonen i Arktis» er på samme måte misvisende. At man ikke med statistisk signifikans kan avvise en pause er ikke det samme som at en pause er påvist. For å gjøre det måtte han påvist at stigningstallet i sist periode er statistisk signifikant forskjellig fra det i første. Det er det ikke.

Til sist, i påstanden «Nesten alle modellene antyder at intern variabilitet i klimaet spiller en viktig rolle i å bremse en menneskeskapte påvirkningen på havisreduksjonen» er ordet «bremse» Østlids eget, og bruken av det er på ingen måte begrunnet hans artikkel. Men ordvalget har som effekt å tone ned faren ved klimaendringene.

Det ville vært mye mer presist å si at naturlige variasjoner av og til bremser, av og til påskynder den menneskeskapte påvirkningen.

Om noen dager vil vi kunne legge til dataene for september 2025. Slik det ser ut i dag (22/9), vil de med overveiende sannsynlig ligge forholdsvis høyt, og dermed bidra litt til å styrke argumentasjoen for en «pause». Men det trengs nok mange flere år før man kan trekke statistisk holdbare konklusjoner.

Videre, for å etablere en pause sikkert bør man ikke bare se på september-data, men hele året, og man bør analysere isvolum på samme måte. Det virker usannsynlig at man innen noen få år kan bekrefte en pause sikkert, for i mellomtiden øker CO2-nivået og dermed oppvarmingen sakte men ubønnhørlig.

Korrigering 13/10-25

Ved en feil gjaldt de 4 plottene som først ble publisert september-minimum og ikke september-middel. Dette er nå korrigert. Forskjellene er små, men synlige. De opprinnelige plottene vises i Appendix under.

Appendiks (13/10-2025): Plot for september-minimum (t.o.m. 2024)

Appendiks (13/10-2025): Plott for september-middel inklusive 2025

Skrevet i Ukategorisert | Legg igjen en kommentar

Ellestad, Klimarealistene og HadCRUT4

Skrevet 26. mai 2025 av A M Raaen

I et innlegg hos Klimarealistene, som er ment å vise at CO₂ er av liten betydning for klimaet, vises denne figuren:

Figur fra Klimarealistene som hevder at temperaturøkningen i HadCRUT 4 var atskillig større fra 1894 til 1953 enn fra 1954 til 2013.

Ellestad oppgir ingen kilde for figuren, men et bildesøk avslører denne kandidaten.

Figuren (basert på HadCRUT4 data) hevder (og Ellestad understreker det i egen tekst) at temperaturen øket atskillig mer i perioden 1894 til 1953 enn i perioden 1953 til 2013.

Men det er et vesentlig problem. Det er gjort på et minutt å plotte dataene f.eks. i Wood for Trees, og få en sterk mistanke om at dette langtfra er korrekt. Med andre ord, Ellestad legger fram figuren uten å ha gjort helt elementær kvalitetssjekking.

La oss se litt nærmere på dette. Her er først et plott av HadCRUT4-dataene i blått, med 10 års glidende middel i gult:

HadCRUT4 månedsdata (blått) og 10-års glidende middel (gult).

Man ser det er mye «støy» i dataene – de er påvirket av kortvarige naturlige fluktuasjoner, mens 10-års glidende middel er mye roligere. Men ser uten videre at fra 10 års middel er det helt klart at temperaturøkningen er større i den siste enn i den første av de to 60-års periodene.

Neste plott viser temperaturendringen 60 år fram i tid, på månedsbasis (x-aksen er starttidspunkt for 60-års perioden). Men ser at verdiene hopper mye fra måned til måned, noe som reflekterer mye kortvarige fluktuasjoner: vær.

HadCRUT4: Temperaturendring 60-år fram i tid, månedsdata.

Figuren under viser dataene for 60-årsperioder med start i årene 1893 og 1894. Blått er månedsdataene, mens gult er det man finner fra 10-årsmiddel. De blå punktene varierer mye fra måned til måned, mens de glattede gule dataene er temmelig konstante. Med andre ord, variasjonen i de blå punktene er knyttet til kortvarige naturlige variasjoner, som snart er positive, snart er negative. Disse kortvarige variasjonene er selvsagt helt uinteressante i forhold til effekten av CO₂, som er forventet å gi langsomme men vedvarende endringer.

HadCRUT4: Temperaturendring 60-år fram i tid, månedsdata. Starttid i 1893 og 1894.

Neste figur viser det samme for 1953 og 1954.

HadCRUT4: Temperaturendring 60-år fram i tid, månedsdata. Starttid i 1953 og 1954.

Man ser at de blå dataene varier så mye at verdiene i Ellestads figur er innenfor variasjonen. Altså, ved litt «snedig» valg av tidspunkt, kan man antagelig ende opp med Ellestads tall. For det er blå punkter under 0.39 i andre periode, og blå punkter over 0.58 i første periode.

Men da får man tall som er dominert av kortvarige fluktuasjoner, som er irrelevant for CO₂-effekten.

De gule midlede punktene varierer lite, og viser at temperaturøkningen i andre periode er rundt dobbelt så stor som i første.

En bedre tilnærming er antagelig å tilpasse en kontinuerlig, stykkevis lineær funksjon til dataene. Dette er vist i figuren under, og man ser at tilpasningen så å si ligger oppå de 10-års midlede dataene.

HadCRUT4 månedsdata (blått) og 10-års glidende middel (gult). Tilpasning til kontinuerlig, stykkevis lineær funksjon i mørkeblått.

Når man har den tilpassede funksjonen, kan man plotte 60-års endringen for hele perioden fra 1850 fram til 1962 (HadCRUT4 dataene slutter i desember 2021), og man finner:

HadCRUT4 månedsdata: Temperaturendring 60 år fram i tid fra den tilpassede stykkevis lineære funksjonen.

Man ser at 60-års temperatur-endring er stigende nesten hele tiden. I 1894 har den verdien 0.31, og i 1954 har den verdien 0.65. Dette viser at Ellestad har gitt helt feilaktige tall («kirsebærplukkede» tall dominert av kortvarige naturlige fluktuasjoner).

Alle kan gjøre en feil. Ellestad har rett i at jeg har «fokusert på en detalj». Men det var helt bevisst, som innledning til mitt spørsmål: «Hvordan kan man stole på andre påstander i innlegget når noe så basalt blir helt galt?»

For hvordan kan man tro at det er seriøs kvalitetsikring, når selv helt enkle bløffer ikke avsløres? Eneste mulige konklusjon er at alle Ellestads påstander må møtes med den største skepsis, og sjekkes i minste detalj!

Skrevet i Ukategorisert | Legg igjen en kommentar

Professor Olav Martin Kvalheim, Klimarealistene og havnivået i Bergen

Skrevet 25. april 2025 av A M Raaen

I et innlegg hos Klimarealistene 21/4-2025 kommer professor Olav Martin Kvalheim med et kraftig oppgjør med en Dagsrevy-reportasje om framtidig havnivå i Bergen.

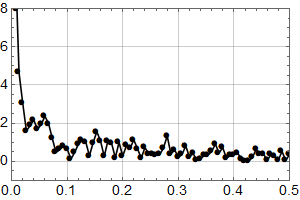
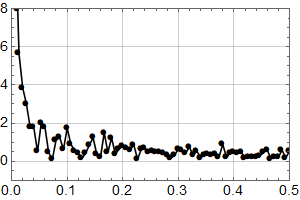
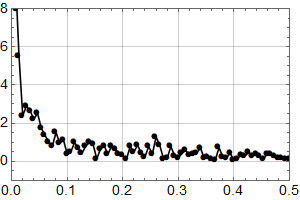
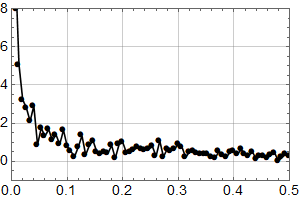
Han harsellerer over prognoser på 40–60 cm stigning ved århundrets slutt, og viser til at om noe har havnivået vært fallende hittil, ihht. en lokal nivåmåler:

Professor Olav Martin Kvalheim presiserer at den negative trenden ikke er statistisk signifikant, slik at man verken kan tolke stigning eller senkning fra disse dataene, og konkluderer:

Så lenge måledata over lange tidsperioder ikke viser endringer, er det absolutt ingen grunn til bekymring for farlig havnivåstigning for Norges del. Dette gledesbudskapet burde NRKs klimaredaksjon og Dagsrevyen sørge for å spre i stedet for å opptre som mikrofonstativ for spredning av spekulative påstander som gjentas og gjentas år etter år

Det kan innvendes at man ikke kan se framover i tid ved å bare se bakover. Men enda større grunn til undring gir det at Olav Martin Kvalheim avslutter sitt plott i 2007 – for nesten 20 år siden! Dette er lett tilgjengelig data, så hvorfor tok han seg ikke det lille ekstra bryet med å lage et oppdatert plott?

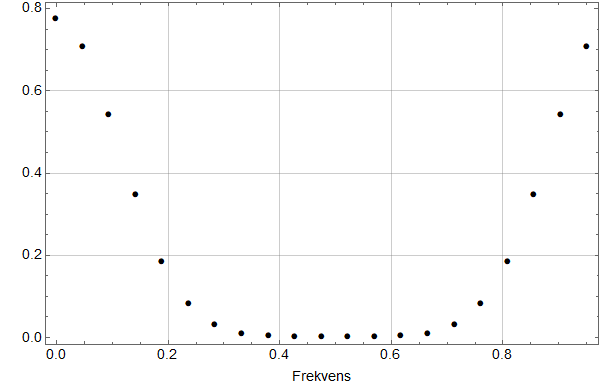
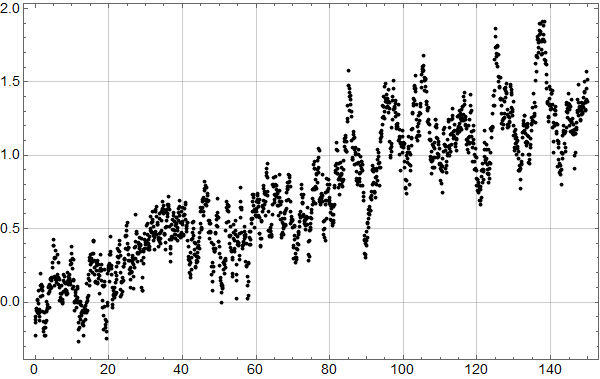
Jeg fant årlige data hos PSMSL.

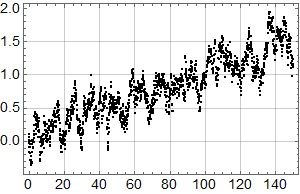
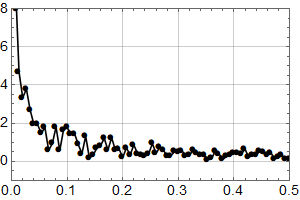
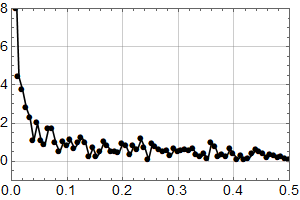
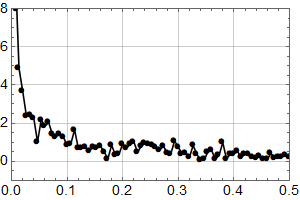
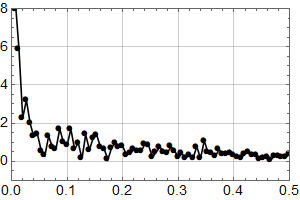
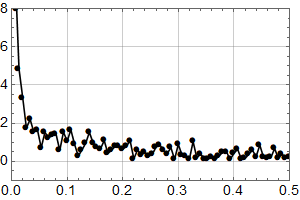
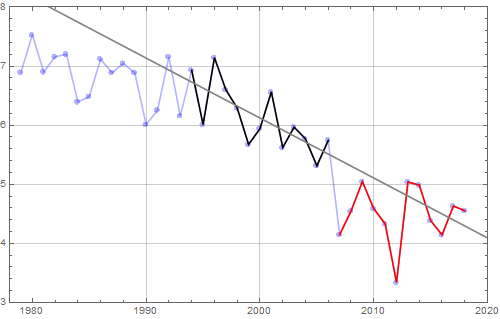
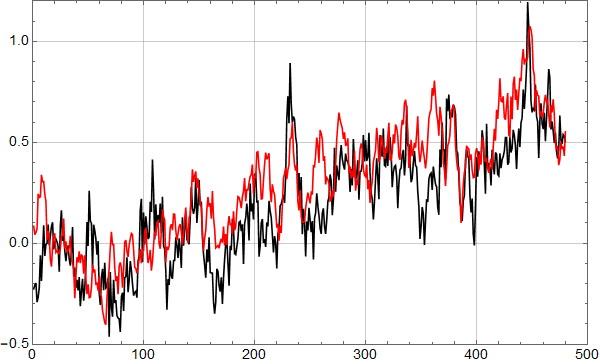
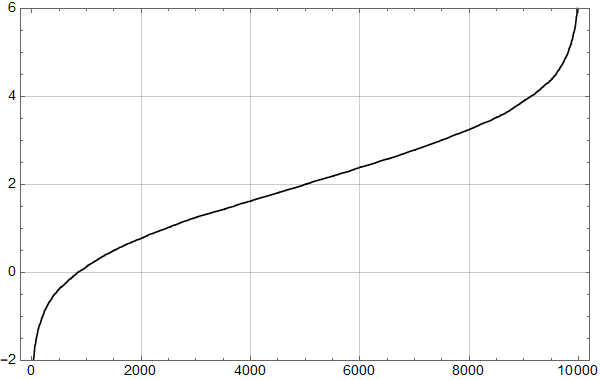
Første skritt er å plotte samme intervall som Olav Martin Kvalheim for visuell sammenlikning:

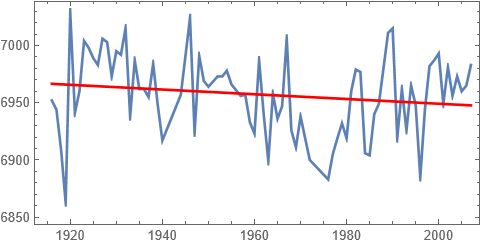
Man ser at selv om det er små forskjeller, er dette samme datasett. Kanskje har det blitt gjort små forbedringer siden 2007? (Man ser også at y-aksen er i mm, og har et ulikt referansenivå, noe som ikke betyr noe for trenden.)

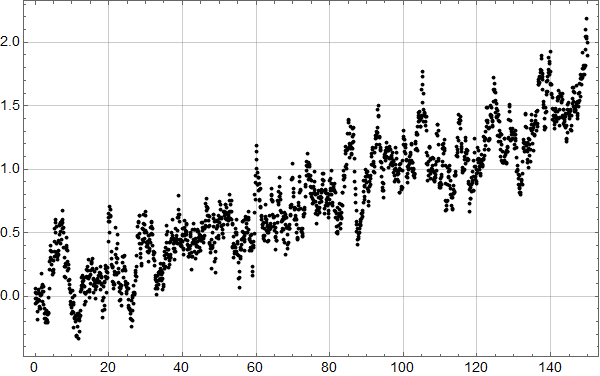
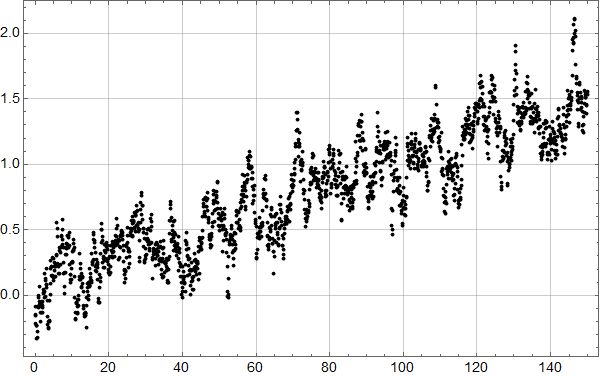
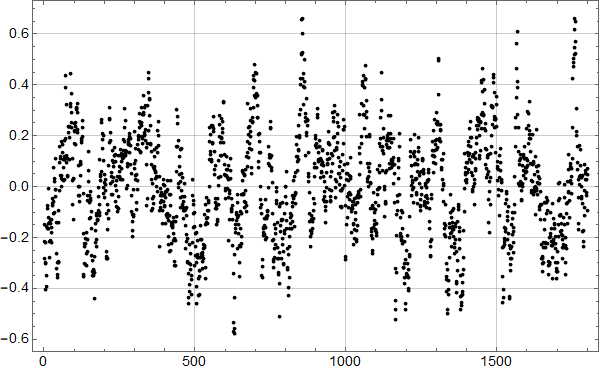
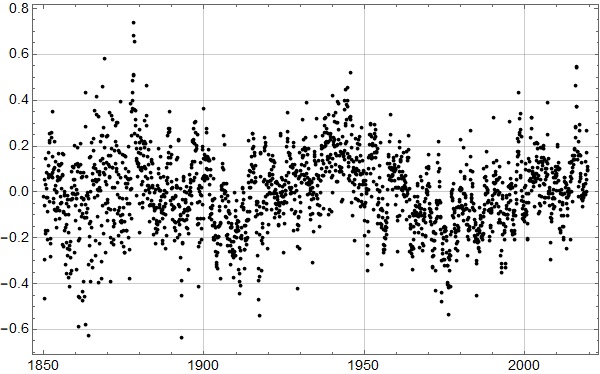
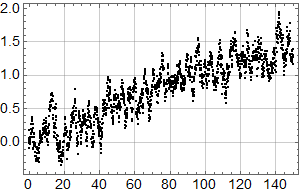
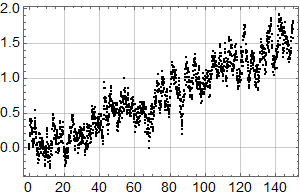
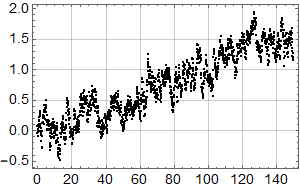
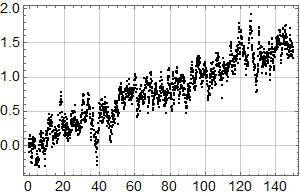
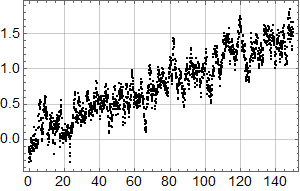
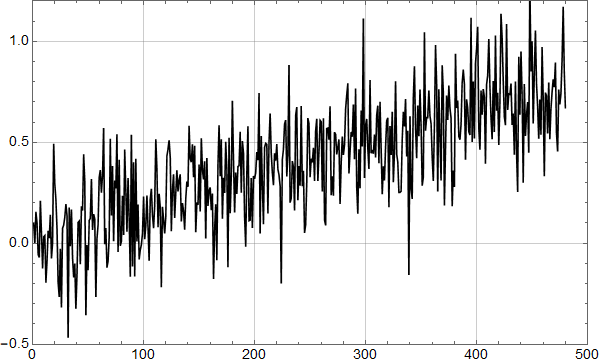
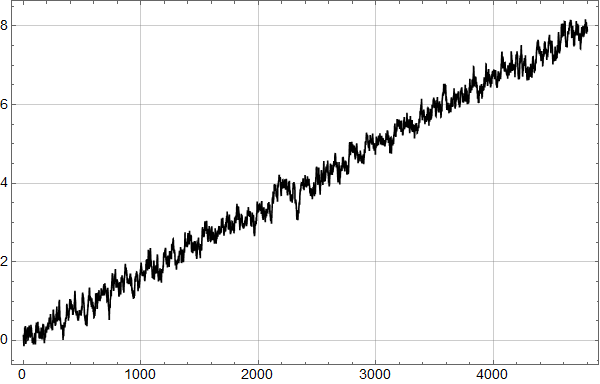
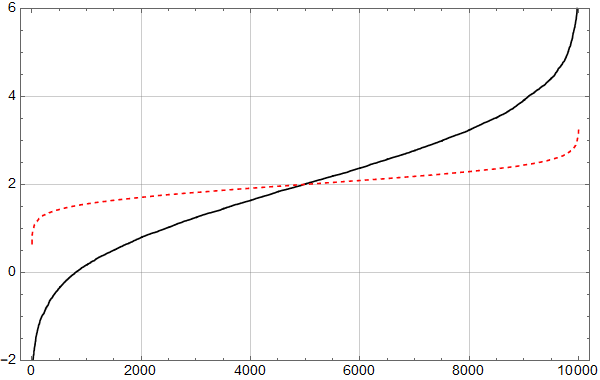
Neste skritt er så å sjekke hvordan trenden fra forrige plott passer med alle dataene:

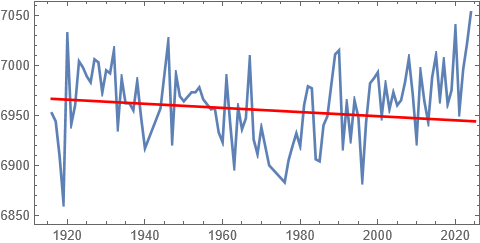
Man ser umiddelbart at det ikke er særlig lurt å kutte ut 18 år med de nyeste dataene: Noe er i ferd med å skje.

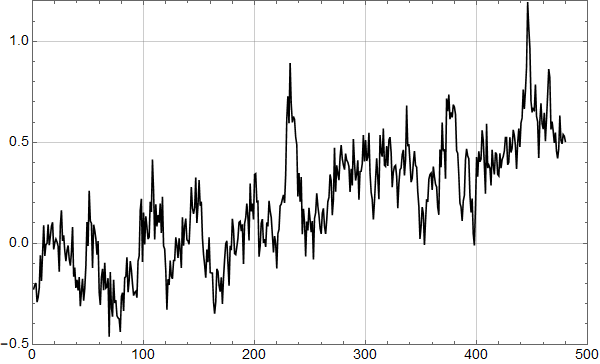
Det kan se ut som om det kan være et trendskifte rundt 1978, med svakt fallende trend før og noe kraftigere stigning etter.

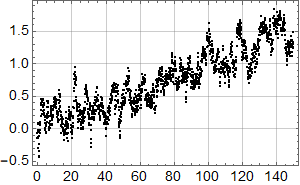
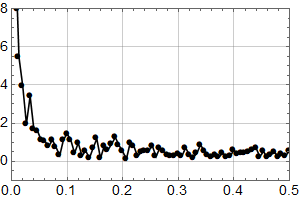
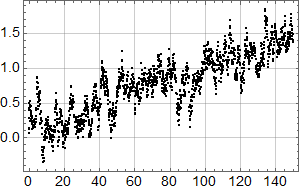
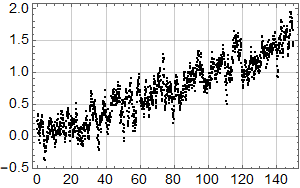
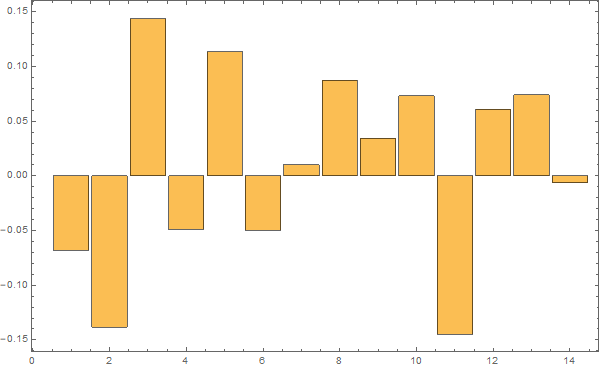
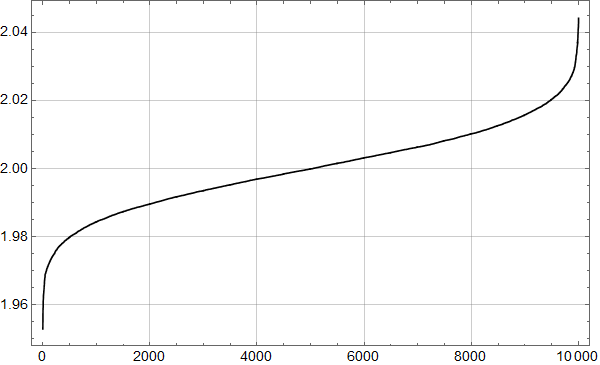
La oss tilpasse en funksjon som består av to rette linjer:

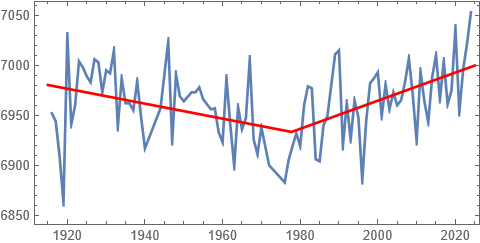
Linjen fram til 1978 faller med omtrent 0,75 mm per år, mens den høyre stiger med 1,4 mm per år. Pga. de store fluktuasjonene er disse tallene usikre, men analysen viser at både fallet før 1978 og stigningen etter er statistisk signifikant, i den forstand at det er mer enn 95 % sjanse for at stigningstallene ikke er lik null.

Siden 1978 har det med andre ord vært statistisk signifikant stigning i det målte havnivået ved måleren i Bergen, så professor Olav Martin Kvalheim har dratt sin konklusjon om det motsatte på sviktende grunnlag.

1,4 mm per år er selvsagt mye mindre enn de 40–60 cm ved slutten av århundret, men man kan ikke bare se bakover når man skal gi en prediksjon. Det kan være mekanismer i gang som fører til en akserelasjon.

Det framstår som stor kontrast mellom professor Olav Martin Kvalheims språkbruk i hans innlegg og hans egen lettvinte omgang med måledataene. Man forventer mer når man signerer som professor!

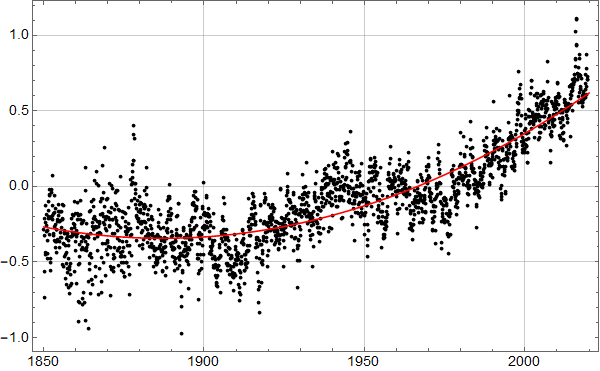
2.ordens tilpasning

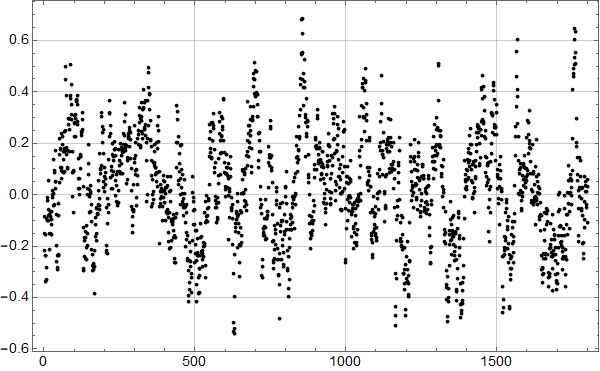
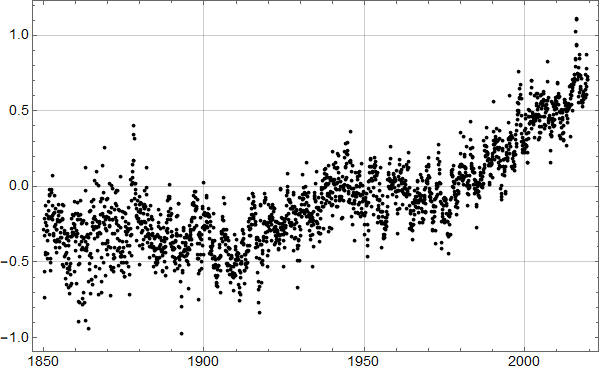
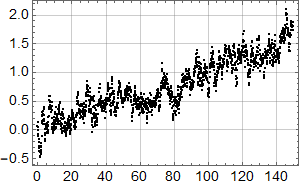
Vi kan selvsagt også tilpasse en andre ordens kurve til dataene. Det ser slik ut:

Den røde kurven har formelen

(1) $\begin{equation*} h(t)=66500 - 60,5 t + 0,0154 t^2 \end{equation*}$

og statistisk analyse viser at det kvadratiske leddet med 95 % sannsynlighet er mellom 0,08 og 0,23. Akserelasjonen ser altså ut til å være statistisk signifikant!

Den røde kurven kan tolkes som å ha to bidrag: Et lineært fallende knyttet til landheving, og et kvadratisk knyttet til havnivåstigning. Hvis vi – noe tilfeldig – antar at den kvadratiske havnivåstigningen startet i 1915 kan vi skrive likningen som:

(2) $\begin{equation*} h(t)=7000 - 1,58 (t-1915) + 0,0154 (t-1915)^2 \end{equation*}$

Denne likningen tilsier en landheving på 1,58 mm, som stemmer godt med den observerte på omtrent 1,5 mm per pr år!

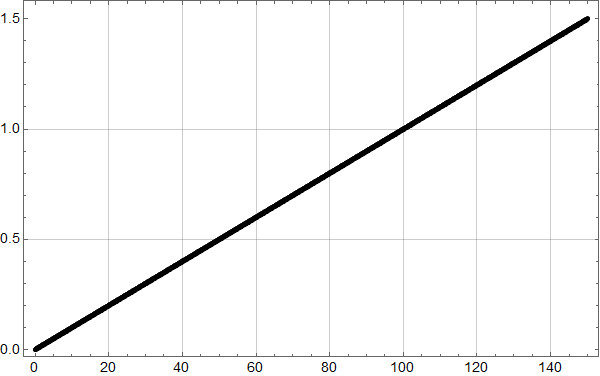
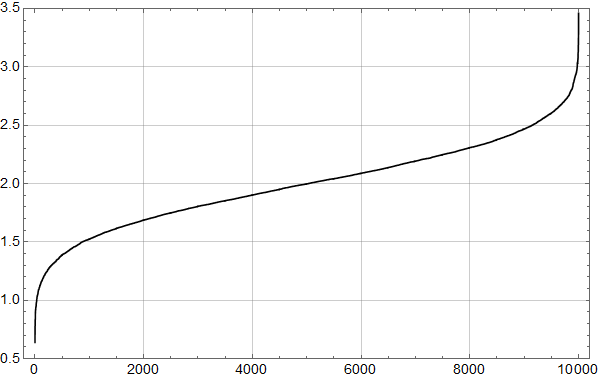
Det er åpenbart at denne argumentasjonen er alt for enkel til å kunne si noe om nivået i 2100. Hvis vi likevel hemningsløst ekstrapolerer den røde kurven, ser det slik ut:

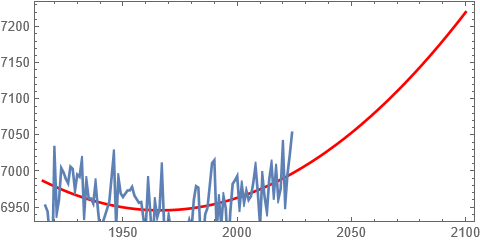
Den røde kurven viser en stigning på over 20 cm fram mot 2100. Det ville være feil å ta det tallet som noen støtte av betydning for klimaforskernes langt mer omfattende modellering.

Men analysen viser en viktig ting: Det er slett ikke rett, som professor Olav Martin Kvalheim hevder, at målingene ved Bergen kan brukes til å avvise klimaforskernes prediksjoner!

Skrevet i Ukategorisert | Legg igjen en kommentar

CO2’s strekkmoder – klassisk tilnærmelse

Skrevet 9. januar 2020 av A M Raaen

Den symmetriske og den asymmetriske strekkmoden innebærer begge vibrasjon langs molekylets akse (se Drivhusgassen CO2, del 1).

Vibrasjonsfrekvensene bestemmes av stivhetene til de to bindingene, som må være like, og massene til atomene.

Man vil da forvente at det må være en sammenheng mellom frekvensene til de to modene, og skal her se på hva en klassisk beskrivelse sier om det.

La oss kalle stivheten for k, massen til O for M, og massen til C for m. La oss videre skrive $u_1$ , $u_c$ og $u_2$ om forskyvningen til de to O-atomene og C-atomet i forhold til likevektsposisjonen.

Newtons 2. lov gir da 3 likninger:

(1) $\begin{align*} M \frac{\mathrm{d}^2 u_1}{\mathrm{d}t^2}&=k (u_c-u_1)\\ m \frac{\mathrm{d}^2 u_c}{\mathrm{d}t^2}&=k (u_1-u_c)+k (u_2-u_c)=k(u_1-2u_c+u_2)\\ M \frac{\mathrm{d}^2 u_2}{\mathrm{d}t^2}&=k (u_c-u_2) \end{align*}$

Vi er interessert i løsninger som vibrerer harmonisk, så vi antar derfor at vi har

(2) $\begin{equation*} u_1(t)=v_1 \mathrm{e}^{i \omega t} \end{equation*}$

og tilsvarende for de to andre. $v_1$ , $v_2$ og $v_c$ er i prinsipp komplekse tall, for å ta hånd om eventuelle faseforskjeller mellom de tre atomene.

Når vi setter inn i likningene over, får vi et resultat som kan skrives som en matrise-likning:

(3) $\begin{equation*} \begin{bmatrix} k -M \omega^2&-k&0\\-k&2k-m\omega^2&-k\\0&-k&k-M\omega^2 \end{bmatrix} \begin{bmatrix}v_1\\v_c\\v_2 \end{bmatrix}=0 \end{equation*}$

Dette er et homogent likningssett, hvor kravet til at det skal finnes løsninger er at determinanten til matrisen er null – matrisen må være singulær.
Dette gir en tredjegradslikning i $\omega^2$ , med løsninger

(4) $\begin{align*} \omega^2 &= 0\\ \omega^2 &= \frac{k}{M}\\ \omega^2 &= \frac{k}{M}\frac{2M+m}{m} \end{align*}$

Når $\omega$ er funnet, kan vi sette den tilbake inn i matriselikningen og finne $v_1$ , $v_c$ , og $v_2$ . Det gir

(5) $\begin{align*} \omega^2 = 0 &:\;\;\; v_1=v_c=v_2\\ \omega^2 = \frac{k}{M}&:\;\;\;v_1=-v_2,\; v_c=0\\ \omega^2 = \frac{k}{M}\frac{2M+m}{m}&:\;\;\; v_1=v_2,\; v_c=-\frac{2M}{m}v_1 \end{align*}$

Den første er homogen translasjon av molekylet uten vibrasjon, den andre er den symmetriske strekkmoden og den tredje er den asymmetriske strekkmoden.

Vi ser at forholdet mellom frekvensene til asymmetrisk og symmetrisk strekk er

(6) $\begin{equation*} \frac{\nu_3}{\nu_1}=\sqrt{\frac{2M+m}{m}}=\sqrt{\frac{2\cdot16+12}{12}}=1,91 \end{equation*}$

Med den asymmetriske moden på 2349 cm^-1 (se Figur 3 i Del3) blir da prediksjonen for den symmetriske moden 1227 cm^-1.

Til sist kan man merke seg at for asymmetrisk strekk har man

(7) $\begin{equation*} M v_1+m v_c + M v_2=\left(2M +m(-\frac{2M}{m})\right)v_1=0 \end{equation*}$

som viser at den asymmetriske moden ikke har total bevegelsesmengde, slik det må være.

Virkelighetens CO₂ er ikke en lineær klassisk oscillator – det må beskrives kvantemekanisk, og det har også bøyemoder. Helt spesifikt kan bøyemoden med 2 kvanter ha samme symmetri som den symmetriske strekkmoden, og energien er omtrent den samme. Disse modene kan derfor «blandes» (Fermiresonans), noe som vil endre energien litt.

Man ser ikke den symmetriske moden direkte i infrarød spektroskopi, men som vi så i Figur 8 i Del 1 ser man den indirekte. Ut fra dette kan man estimere forventede frekvenser:

667 cm^-1 + 618 cm^-1= 1285 cm^-1 og 667 cm^-1 + 720 cm^-1 = 1387 cm^-1 der 667 cm^-1 er senterfrekvens til bøyemoden.

I Raman spektroskopi forventer man altså topper rundt 1285 cm^-1 og 1387 cm^-1 for CO₂

Skrevet i CO2, Ukategorisert | Legg igjen en kommentar

Drivhusgassen CO₂ – Del 3

Skrevet 29. desember 2019 av A M Raaen

I Del 1 så jeg på den delen av det infrarøde spektert til CO₂ som er viktig for drivhuseffekten – dvs. i hovedsak bøyemoden. I Del 2 så jeg litt på konsekvenser for transmisjon av stråling i atmosfæren.

I denne delen ser jeg på hele spekteret til CO₂, dvs. også de delene som er av liten betydning for drivhuseffekten. Vi ser på CO₂‘s svake absorpsjon i «det atmosfæriske vindu»; disse linjene er viktig for en teknisk anvendelse – CO₂-laseren, og vi ser på frekvensområdet hvor OCO-2 – satellittbasert måling av CO₂-nivået – arbeider.

Oversikt

Databasen HITRAN inneholder i alt 173024 spektrallinjer fra 158.301811 cm^-1 til 14075.298241 cm^-1. (Det tallet inkluderer bare isotopene det er mest av, ¹²C og ¹⁶O; tar man med alle kombinasjoner av isotoper er tallet 559874.)

Figur 1 viser en oversikt – vi ser at det er tre områder som har spesielt sterke linjer. Lengst til venstre er bøyemoden, som vi så på i del 1. I midten er den sterkeste, asymmetrisk strekk, og til høyre en kombinasjon av symmetrisk og asymmetrisk strekk. Øvrige linjer ligger i dette plottet helt nede på y-aksen.

Man kan merke seg at området fra 1199.6 cm^-1 til 1420.8 cm^-1 er helt uten spektral-linjer (fra del 1 husker man at den symmetriske moden har energi rundt 1340 cm^-1)

Figur 2 viser det samme, men med logaritmisk y-akse, hvor de svake linjene kommer klarere fram.

Asymmetrisk strekk

Av figur 1 og 2 ser vi at dette er den mest intense moden – omtrent 10 ganger sterkere enn bøyemoden. Den er likevel av beskjeden betydning for drivhuseffekten på jorden, siden den er utenfor varmespekteret (se figur 2 i del 1). Se Figur 3 i del 1 for illustrasjon av vibrasjons-modene.

Figur 3 viser spektralområdet rundt 2350 cm^-1, dvs. asymmetrisk strekk mode. Én mode dominerer – det er overgang mellom vibrasjons-grunntilstand og ett kvant i asymmetrisk strekk, men vi ser også en rekke svakere linjer.

Figur 4 viser hovedmoden, med P- og R-gren i ulik farge. Merk at Q-grenen er fraværende – dette skyldes at asymmetrisk strekk ikke har noen dreieimpuls, og fotonet må dermed få sitt spinn fra endring i rotasjons-nivået til CO₂.

Figur 5 viser den nest sterkeste moden. Den skyldes at CO₂-molekyler som har ett kvant i bøyemode i tillegg får et kvant i asymmetrisk strekk. Her ser man en svak Q-gren i tillegg til P- og R-grenene.

Hvis man fjerner linjene fra Figur 4 og 5, ser området rundt 2350 cm^-1 ut som vist i Figur 6. Man ser 3 ulike moder som er sterkere enn de øvrige.

Figur 7 viser de tre sterkeste modene fra Figur 6 i hver sin farge. De oransje og blå punktene er Fermiresonanser av 2 kvanter i bøy og en kvant i symmetrisk mode, som eksiteres videre med ett kvant i asymmetrisk strekk. Man ser at Q-grenene mangler, av samme grunn som for fundamental asymmetrisk strekk.

Den grønne linjen er to kvanter i bøyemoden, med dreieimpuls 2, som eksiteres videre med ett kvant i asymmetrisk strekk. Her er Q-grenen tillatt, men svak. Legg merke til at det er dobbelt så mange punkter i den grønne – dette skyldes at alle rotasjonskvantetall er tillatt for denne, men bare like kvantetall er tillatt i slutt-tilstanden for de to andre.

CO₂s absorpsjon i «det atmosfæriske vindu»

«Det atmosfæriske vindu» er en betegnelse på området omtrent 800-1200 cm^-1 (omtrent 8 µm til 12 µm bølgelengde) hvor en normal jordisk atmosfære har liten absorpsjon – dvs at stråling fra overflaten har stor sjanse for å nå verdensrommet.

CO₂ har noen svake linjer i området, som vist i Figur 8.

Figur 9 viser transmisjon gjennom en 10000 m tykk atmosfære med 400 ppm CO₂, trykk 1 bar og temperatur 0 °C, beregnet med HAPI. Dette svarer omtrent til rett antall molekyler i en kolonne i vår atmosfære, men trykk og temperatur-profilene er ulike. Spesielt er temperatur viktig, siden utgangspunktet for absorpsjonen er en eksitert tilstand, hvor populasjonen øker med økende temperatur. Dette betyr at figur 9 viser mindre transmisjon enn det som skjer i atmosfæren.

På Venus, hvor atmosfæren er dominert av CO₂, og trykket og temperaturen er mye høyere, er disse frekvensområdene fullstendig i metning.

Digresjon: CO₂-laseren. CO₂ laseren utnytter de to Fermi-resonanslinjene vist med grønt og rødt. Laseren virker ved at N₂ molekyler eksiteres (vibrasjonsmode) med kollisjon med elektroner, og de overfører så sin energi til den asymmetriske strekkmoden i CO₂ ved kollisjon, som gjør at denne moden har mye større populasjon enn ved termisk likevekt, og laseren fungerer på vanlig måte via stimulert emisjon.

OCO-2

Orbiting Carbon Observatory 2 måler CO₂-nivået ved registrere hvordan sollys reflektert fra overflaten absorberes av CO₂. Dette skjer ved å måle på to frekvenser, ca 4850 cm^-1 (bølgelengde 2.06 µm) og ca 6220 cm^-1 (ca 1.61 µm). I tillegg måles oksygen’s A-bånd på ca 13100 cm^-1 (0.765 µm) for kalibrering.

Figur 10 viser en oversikt over CO₂‘s absorpsjon i frekvensområdet 4000-7500 cm^-1, mens figur 11 og 12 viser de to aktuelle enkeltmodene.

Figur 13 viser transmisjon gjennom en 10000 m tykk atmosfære med 400 ppm CO₂, 1 bar trykk og temperatur 0 °C.

Oksygens absorpsjon er knyttet til endringer i molekylets elektronkonfigurasjon. O₂ har 2 ytre elektroner (valenselektroner) i orbitaler som har plass for 4 elektroner. Dette betyr at spinnene til to ytre elektronene kan peke i samme retning, eller i motsatt retning. I henhold til Hunds regler er grunntilstanden med spinnene i samme retning. Det betegnes triplett tilstand, siden energinivået splittes i 3 i et magnetfelt.

Det finnes to tilstander der spinnene peker i motsatt retning, den laveste kalles singlett oksygen. Begge de to singlett-tilstandene gir opphav til absorpsjonslinjer idet oksygen går fra grunntilstanden og opp. Som for CO₂ påvirkes linjene av rotasjon, men også av vibrasjon.

Figur 14 viser i blått overganger knyttet til den laveste singlett-tilstanden, og i gult de som er knyttet til den øverste. De sterkeste linjene, ved knapt 8000 cm^-1 og rundt 13000 cm^-1 er overganger uten endring i vibrasjon, mens gruppene på hver side innebærer overganger med samtidig endring i vibrasjon. Internt i gruppene er det struktur knyttet til oksygens rotasjons-nivåer, samt overganger med eksiterte vibrasjonstilstander som ikke endrer seg.

Den sterkeste linjen, ved ca 13000 cm^-1 benevnes for oksygens A-bånd, og er den OCO-2 måler.

Skrevet i CO2, Klima | Legg igjen en kommentar

Sykler i syntetiske data?

Skrevet 29. september 2019 av A M Raaen

Torsdag 19 september 2019 14:58 viste Leif Liland på Terje Wahls blogg denne figuren for HadCrut 3 data.

Her er diverse sykler angitt, 60 år, 20 år osv.

Jeg spurte meg derfor: Kan man se sykler i syntetiske data – hvor man vet de ikke finnes?

Men før man går i gang med å Fourier-transformere reelle data, eller syntetiske data som likner på reelle, kan det være greit å se på noen enkle eksempler, for å få en idé om det er fallgruver man kan gå i.

For å følge argumentasjonen under er det nødvendig med litt kjennskap til hvordan svingninger og bølger beskrives med komplekse tall.

Første figur viser en gauss-puls i tidsplanet som er digitalisert i punkter med lik avstand.

Neste figur viser den Fourier-transformerte slik den vanligvis framstilles. Siden koeffisientene er komplekse tall, har jeg plottet absoluttverdien. Det er like mange punkter som i tidsplanet.

Her kan man undres hvorfor det er frekvenser opp mot 1 – det er jo klart at frekvensene i tidssignalet er lavere. Oppklaringen er at digital Fourier transform (DFT) bare skal regne tilbake for de opprinnelige tids-punktene. Prøver man å beregne mellomliggende punkter direkte basert på DFT-dataene, vil en få komplekse tall.

Siden man kan bare skal «treffe» de opprinnelige punktene kan man multiplisere med et signal som har samme verdi i alle punktene – en sinus som gjør en hel eller flere hele perioder mellom hvert opprinnelige punkt i tidsplanet.

I praksis betyr det at man kan flytte de digitale punktene opp eller ned (en eller flere ganger) med totalt antall punkter.

Det mest logiske er å flytte øvre halvdel nedover. Da får man et signal som er symmetrisk om null frekvens, som vist i neste figur. Den heltrukne kurven er en gaussisk puls – som er i tråd med at den Fourier transformerte av en gaussisk puls er en gaussisk puls i frekvensplanet.

I dette plottet er koeffisientene for en positiv og tilhørende negativ frekvens de kompleks konjugerte av hverandre. Det betyr at når de summeres får man alltid et reelt signal, og man kan bruke dataene på denne formen til å interpolere mellom de opprinnelige punktene i tid.

Koeffisienten for null frekvens er reell, og er et mål for middelverdien av signalet i tidsplanet.

På grunn av symmetrien mellom positive og negative frekvenser, kan vi nøye oss med å plotte de positive. Det gjøres i det følgende.

Neste figur viser en hel periode av en sinus-kurve med frekvens 0,1, digitalisert med 11 punkter med samme avstand.

Den digitale Fourier-tranformasjonen ser slik ut:

Her er det flere ting som i første omgang kan se overraskende ut: Vi har ikke noe punkt på 0,1 – frekvensen til sinusbølgen, og det er flere andre frekvenser som også er ulik null.

Oppklaringen er enkel, men vesentlig: Hver enkelt frekvens beskriver en uendelig sinusfunksjon. Men et endelig antall frekvenser kan man bare beskrive en periodisk funksjon, dvs en funksjon som gjentar seg selv om og om igjen.

Vi ser at dataene både starter og slutter med en null. Når vi gjør dette periodisk, får vi 2 nuller på rad: Vi har ikke lenger en ren sinus.

Neste figur viser punktene for 2 perioder, og med blått viser resultatet av den inverse fourier-transformasjonen, også for mellomliggende punkter. Det er tydelig at dette ikke er en ren sinus – noe som stemmer med at vi hadde flere frekvenser ulik null.

Ved å droppe det siste punktet, får vi en sekvens som kan skjøtes sammen til en ren sinus.

Og ganske riktig: Vi får da bare én frekvens, den riktige på 0,1.

Dette er et viktig poeng: En digital Fouriertransform antar implisitt at tidssekvensen den brukes på er periodisk!

La oss se hvordan det virker for en lineært økende kurve – som Fouriertransformasjonen altså ser på som en periodisk sag-tann kurve. Den stiger jevnt, men faller brått tilbake til startpunktet for hver periode.

her er den digitale Fourier transformasjonen

og neste figur viser hvordan Fourier dataene med interpolasjon blir i tidsplanet, for 2 perioder. De opprinnelige dataene vises som svarte punkter.

La oss så se på en dataserie med månedlige data over 150 år, som stiger til sammen 1,5 grader:

Den Fourier transformerte (opp til f=0.5 per år) er (punktet for f=0 faller utenfor plottet – det er middelverdien og dermed ikke så interessant).

Man kjenner igjen økningen under 0,1 fra det første plottet for HadCrut 3 dataene!

Etter denne innledningen er man bedre rustet til å se på syntetiske data. Her er 3 realisasjoner av en AR(1) prosess med lineær stigning 1 grad per hundre år samt støy med autokorrelasjonskoeffisent 0,92 og standardavvik 0,2:

Realisasjonene er ikke tilfeldig valgt – jeg har sett etter eksempler som likner de reelle dataene. Men se helt nederst for 10 tilfeldige realisasjoner.

Realisasjon 1:

Realisasjon 2:

Realisasjon 3:

Vi ser at kurvene øker mot null frekvens som for den lineære uten støy, og man ser at kvalitativt kan man tolke omtrent like mye sykler som i HadCrut3 dataene vi startet med. Men vi vet altså med sikkerhet at det ikke er deterministiske sykler i de syntetiske dataene – kun tilfeldig statistisk variasjon.

Konklusjonen må bli at man ikke kan konkludere sikkert med sykler fra HadCrut 3 plottet heller.

De neste figuren viser hvordan det går når vi fjerner den underliggende trenden i realisasjon 3.

Først bruker vi trenden som ble brukt da dataene ble generert:

Man ser at stigningen mot null frekvens er borte.

Neste 2 plott viser hvordan det går når man bruker lineær trend bestemt med minste kvadraters metode. Forskjellen er ubetydelig – som man kunne vente.

Hva så med HadCrut 4?
Neste figur viser globale HadCrut4 data lastet ned fra WoodForTrees 1. oktober 2019.

Neste figur viser spekteret. Ingen helt åpenbare sykler, men vi ser den ventede stigningen mot null frekvens – den er et resultat av differensen mellom 2019 og 1850.