Drivhusgassene er avgjørende for jordas klima ved at de bestemmer fra hvilken høyde i atmosfæren varmestråling unnslipper til verdensrommet.
I dette innlegget tar jeg for meg CO2 i større detalj enn man vanligvis ser. Dette er derfor et langt innlegg, fordi en gjennomgang av en del grunnleggende stoff er nødvendig. Hvis noe virker vanskelig, er det viktig å ha klart for seg at jeg bare skraper i overflaten av det fysikken kjenner til om CO2’s egenskaper.
Det er ikke nødvendig å ha en så detaljert kjennskap til CO2 for å forstå drivhuseffekten – det er helt greit å tenke at dette er veletablert fysikk som ekspertene har full kontroll på.
Men i en tid hvor effekten tidsvis framstilles som «CO2-hypotesen» eller «CO2-myten» kan det vel være greit å ha en liten følelse for hva som ligger av veletablert fysikk i dette.
Varmestrålingsspekteret
Drivhusgassene stopper og sender ut igjen varmestråling fra jordoverflaten. For å beskrive effekten, er det derfor nødvendig å vite i hvilken del av det elektromagnetiske spekteret varmestrålingen skjer.
Figuren under viser intensiteten av varmestråling som funksjon av bølgelengde, antatt at temperatur på legemet er 14 °C (som omtrentlig er jordoverflatens middeltemperatur).
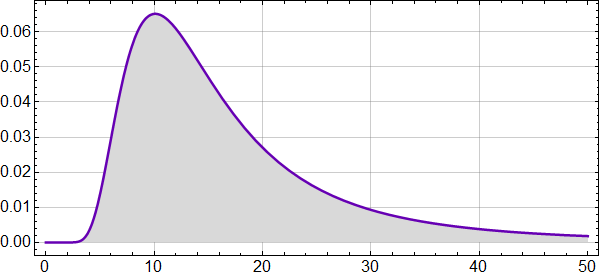
Topp-punktet på rundt 10 mikrometer svarer til en frekvens på 3×1013 hertz, dvs 30 terahertz – 30 billioner svingninger i sekundet. (Til sammenlikning jobber mobilnettet rundt 2 gigahertz – 10000 ganger lavere frekvens.)
Figuren forteller oss at det aller meste av varmestrålingen ligger for bølgelengder mellom 3-4 mikrometer og 50 mikrometer.
Fysikerne foretrekker ofte å arbeide i frekvens heller enn i bølgelengde. En fordel er f.eks. at energien til et foton er direkte proporsjonal med frekvensen. Men det er upraktisk å arbeide med tall av størrelse 3×1013, så i infrarødspektroskopien er det lang tradisjon for å måle frekvens på en alternativ måte: I stedet for å telle antall svingninger per sekund, teller man antall bølgelengder per cm. Man får da et frekvensmål – benevnt som inverse centimeter eller cm-1 som gir mer praktiske tallverdier. Så kan man lett konvertere til det vanlige frekvensmålet ved å multiplisere med lyshastigheten målt i centimeter per sekund: 3×1010 cm/s.
Figuren under viser varmestrålingsspekteret ved 14 °C plottet mot frekvens i inverse centimeter.
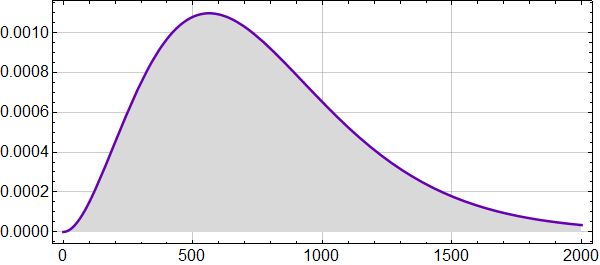
Varmestrålingens vekselvirkning med materien
Varmestrålingen er elektromagnetisk stråling – på samme måte som lys og radiobølger. Elektromagnetisk stråling vekselvirker med materien via ladninger. Om materien et helt nøytral – ikke har noen ubalanse i ladning – vil det ikke være noen vekselvirkning med stråling.
Ladningsfordelingen i CO2-molekylet
CO2 består av et C-atom og to O-atomer på en rett linje. O-atomene trekker litt mer på elektronene enn C-atomet, slik at de er litt negative, mens C er litt positiv. Men pga av symmetrien, O-ene ligger helt likt i forhold til C blir nettoeffekten null – det er ingen ladningsubalanse som et eletromagnetisk felt kan vekselvirke med.
CO2 kan derfor bare vekselvirke med varmestråling om noe bryter symmetrien: molekylet må vibrere.
CO2s vibrasjonsmoder
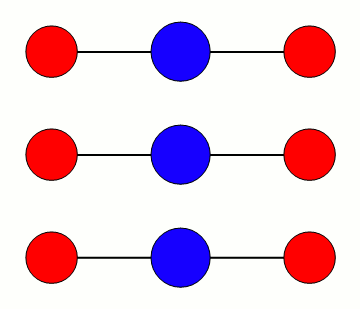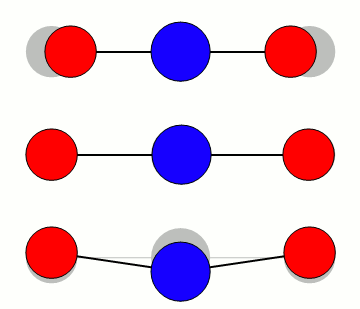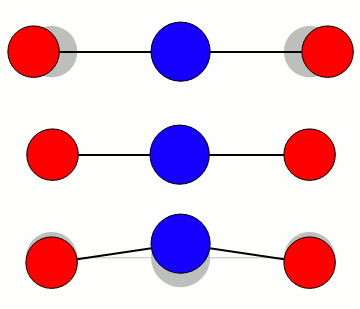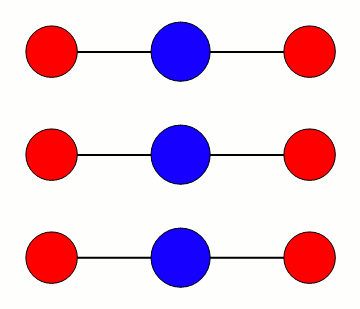
De tre modene er illustrert med omtrentlig riktig relativ frekvens. Bøyemoden vibrerer rundt 667 cm-1, altså omtrent 20 terahertz, mens den asymmetriske moden er nær 2350 cm-1 eller 70 terahertz. I bølgelengde er det henholdsvis 15 mikrometer og 4,2 mikrometer. Den symmetriske moden er rundt 1340 cm-1, eller omtrent 7,5 mikrometer/40 terahertz.
Ved å sammenlikne med figuren over for varmestrålingens fordeling, ser en umiddelbart at det er bøyemoden som er viktigst for CO2’s virkning som drivhusgass. Den asymmetriske strekk-moden er så høyt i frekvens at det er lite varmestråling å vekselvirke med for temperaturene vi har på jorda.
Vibrasjon og rotasjon
CO2 kan ikke bare vibrere – den kan også rotere – noe som fører til modifikasjoner av spekteret, av to hovedgrunner:
- CO2 kan endre sin rotasjonstilstand samtidig som vibrasjonstilstanden endres
- Rotasjonen påvirker vibrasjonen – slik at energien i en vibrasjonsovergang er avhengig av rotasjonstilstanden
For å gå nærmere inn i dette må vi se litt på to kvantemekaniske modell-systemer: den harmoniske oscillator og den stive rotator.
Harmonisk oscillator
Den harmonisk oscillator er den enkleste kvantemekaniske modellen for et system som vibrerer. Den har energinivåer gitt ved
E = konst (n + 1/2)
der n er et heltall som kan ta verdier 0, 1, 2, 3 osv.
Det er to ting å merke seg: Selv om vi setter inn n=0 får vi en energi ulik null. I motsetning til en makroskopisk vibrasjon kan ikke den kvantemekaniske være i ro!
Avstanden mellom nivåene er like: Det er like stor forskjell på nivå 0 og 1 som det er på 1 og 2 osv.
Merk: Energien kan bare ha de spesifikke verdiene gitt av formelen over – den kan ikke ta mellomliggende verdier.
Et CO2 molekyl får sin vibrasjon fra kollisjoner med andre molekyler eller fra stråling. Hvor mange vibrasjonsnivåer som er aktive kommer an på energien tilgjengelig – dvs på temperaturen.
For bøyemoden til CO2 ved romtemperatur er nesten alle molekylene i tilstanden n=0, det er kun 3-4 % i n=1 og rundt en promille i n=2.
Stiv rotator
Energinivåene er generelt
E = konst L(L+1)
der L er et heltall som tar verdiene 0, 1, 2, 3 osv.
konst er omvendt proporsjonal med det som kalles treghetsmomentet til molekylet – et mål på hvor langt massen er fra sentrum.
Vi ser at her øker avstanden mellom nivåene med L – i motsetning til oscillatoren hvor de var uavhengig av n.
For vibrasjonsgrunntilstanden til CO2 er bare like tall tillatt.
Rotasjonsenergien er mye mindre enn vibrasjonsenergien – det betyr at kollisjoner med andre molekyler fører til at mange ulike rotasjonsnivåer er besatt.
Innledningen er ferdig!
Vi har nå vært gjennom det nødvendig grunnlaget:
- Det mye brukte frekvensmålet inverse centimeter
- CO2’s «infrarøde egenskaper» er relatert til vibrasjoner og rotasjoner
- For vibrasjoner er det primært grunntilstanden som er aktiv, mens mange rotasjonsnivåer er aktive.
- Det er særlig CO2’s bøyemode som bidrar innenfor varmestrålingsspekteret
La oss se litt mer detaljert på CO2’s bøyemode!
OVERSIKT over CO2’s bøyemode
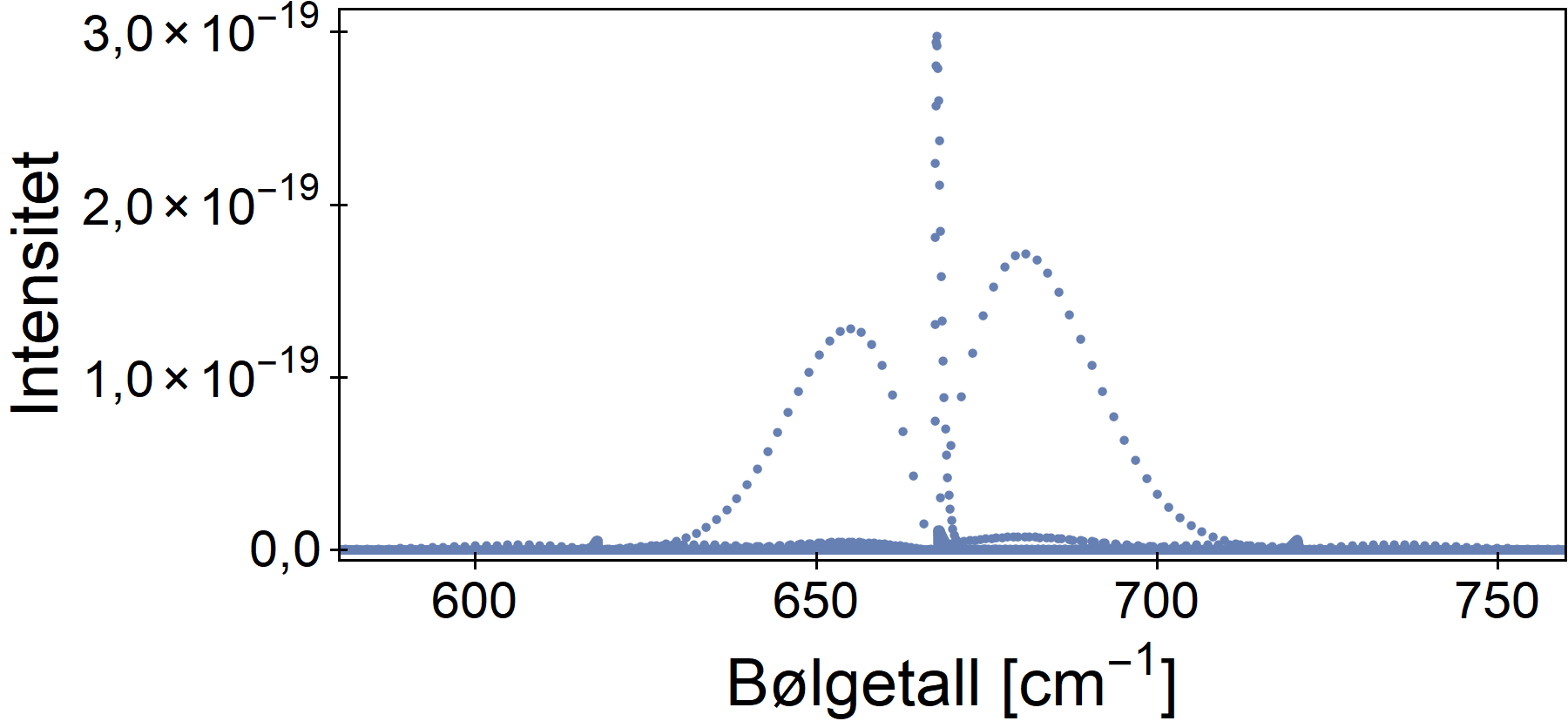
Figuren viser en oversikt over bøyemoden. Vi ser en skarp «pigg» i midten, og to mer avrundede høyder på hver side. Dette utgjør til sammen den fundamentale bøyemoden.
Man ser videre en del punkter nær x-aksen som er mye svakere – dette har med høyere vibrasjonsmoder å gjøre.
På flankene – ved ca 620 og ca 720 inverse centimeter ser man to små topper – vi kommer tilbake til dem.
(begrepet bølgetall i figurene er i prakis det samme som frekvens.)
Q-grenen til den fundamentale vibrasjonsmoden
Figuren under viser et mer detaljert plott av den «skarpe piggen» fra oversiktsplottet.
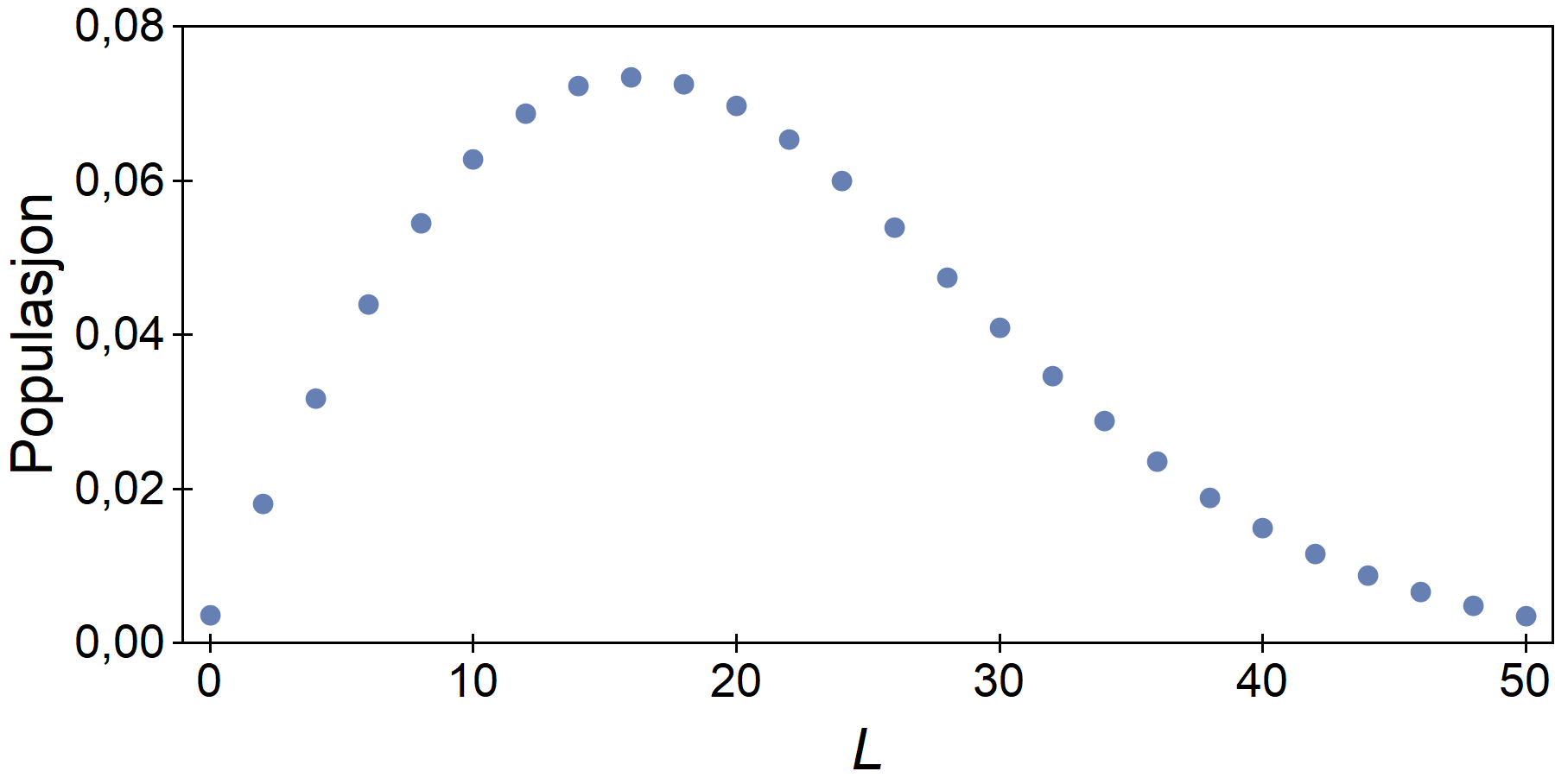
Denne svarer til endring i vibrasjon uten samtidig endring i rotasjon. Det er likevel mange punkter – svarende til ulike rotasjonsnivåer – fordi vibrasjonsenergien er litt avhengig av rotasjonstilstanden. Dette betegnes som Q-grenen. Legg merke til at intensiteten er sterkest for L=16 – det skyldes at dette rotasjonsnivået er mest «befolket».
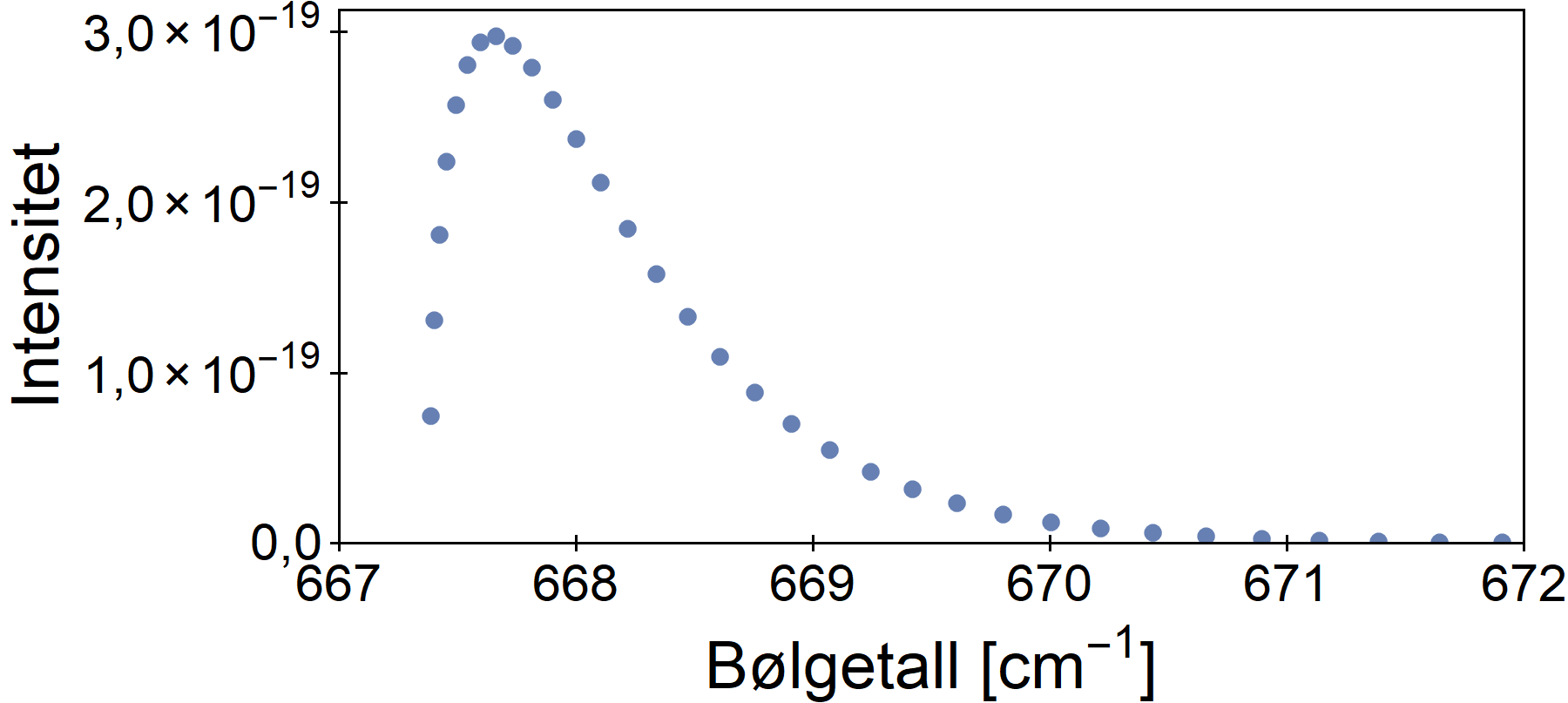
P- og R-grenene til den fundamentale vibrasjonsmoden
Dette er de to dominerene flankene i oversiktsfiguren. De svarer til at rotasjonstilstanden endrer seg med pluss eller minus én samtidig som vibrasjonstilstanden endrer seg. Intensiteten er sterkest for L=16.
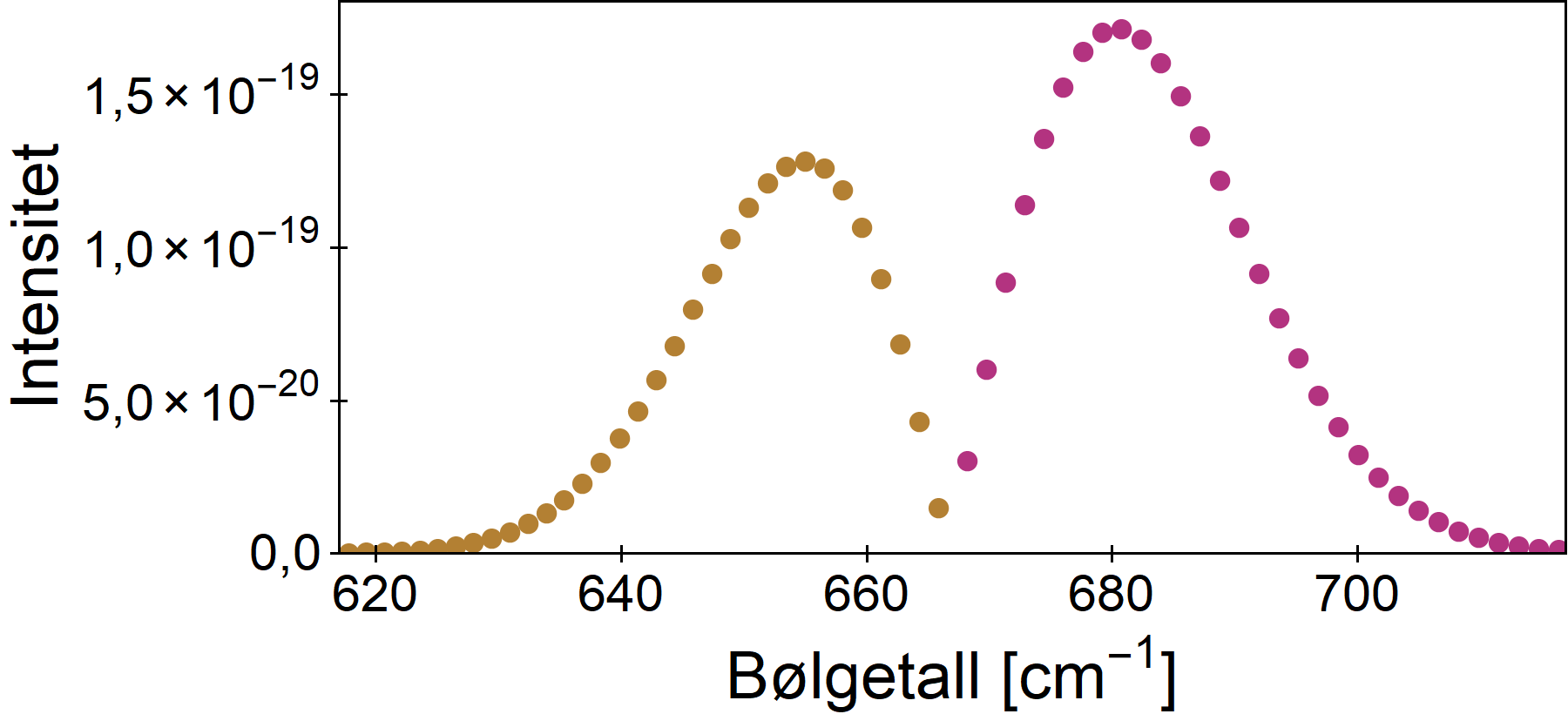
Eksempel på høyere ordens moder
Dette er de to små toppene som knapt var synlige i oversiktsfiguren, og skyldes vibrasjonsovergang fra bøyemoden til den symmetriske strekkmoden. Det er to topper, og i hver av dem kjenner man igjen Q-, P- og R-grener. Som før er hver gren mest intens for L=16.
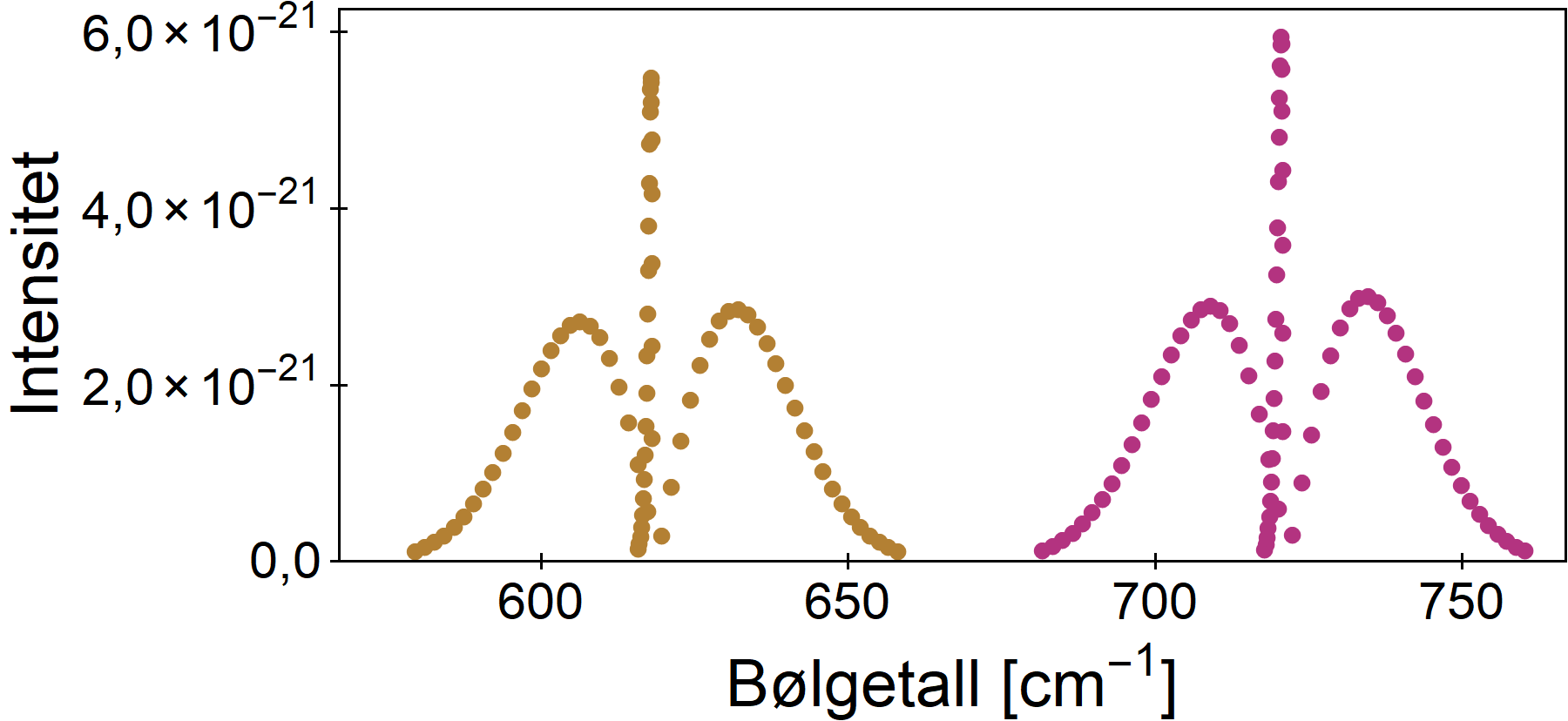
Oppsummering
Vi har overfladisk gått gjennom aspekter ved infrarød-spekteret til CO2. Vi har sett at for hver eneste frekvens hvor CO2 er aktiv, kan vi detaljert knytte dette til en spesifikk vibrasjons- og rotasjonstilstand.
Rotasjoner er viktige – de bidrar til å gjøre den totale linjen mye bredere.
Man kan trygt si at spekteret er forstått i nær full detalj – for bak denne forenklede framstillingen ligger mange høyteknologiske målinger og mye avansert matematisk tolkning og modellering.
Tillegg 21/11-18: To kvanter i bøyemoden
Den oppmerksomme leser vil se at det er «noe» nede ved aksen, rundt 670 cm-1, i Figur 5 – oversikten over bøyemoden til CO2.
Her er dette forstørret:
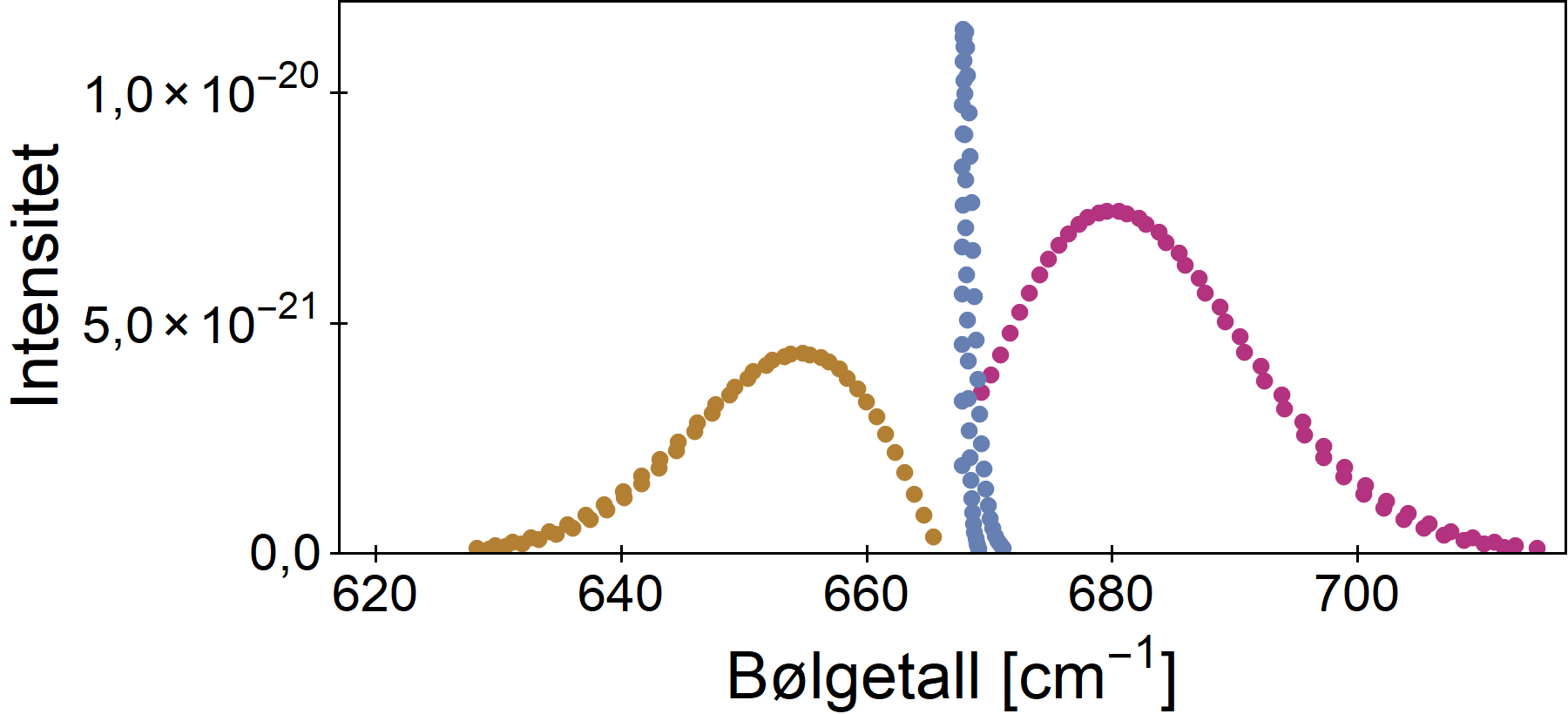
Dette dreier seg om at molekylet går fra ett til to kvant i bøyemoden. Man kjenner igjen P-, Q- og R-grener.
Studerer man figuren nøyere, ser man at det egentlig er to sett punkter i hver gren – dette er relatert til hhv odde og like rotasjonskvantetall.
I vibrasjons-grunntilstanden er bare like rotasjonskvantetall tillatt av symmetrigrunner, men denne begrensningen gjelder ikke for eksiterte tilstander.
Legg merke til at høyden på toppen er 25–30 ganger mindre enn for hovedlinjen. Dette skyldes (som nevnt over) at bare 3–4 % av CO2-molekylene er i første eksiterte tilstand ved romtemperatur. Om man øker temperaturen, vil balansen forskyve seg, og høyere ordens linjer vil bli relativt sterkere. Disse høyere ordens linjene betegnes derfor «hot bands» på engelsk
Tillegg 23/11-2018: Kilder
Tabellene man får ut innholder en rekke parametre som er nødvendig for full beskrivelse av absorpsjonslinjene. I dette innlegget har vi brukt bare noen få av dem:
- frekvens i cm-1
- linje-intensitet (ved 296 K)
- kvantetall for start- og slutttilstander
«Global» og «Local» «Upper» and «Lower quanta» varierer med hvilket molekyl man ser på.
For CO2 er «Global quanta» knyttet til vibrasjon, og består av 5 kvantetall:
- ν1 – Kvantetall for symmetrisk strekk
- ν2 – Kvantetall for bøyemoden
- l – Kvantetall for bøyemodens bidrag til dreieimpulsen
- ν3 – Kvantetall for asymmetrisk strekk
- r – Kvantetall for ordning av linjer knyttet til Fermi-resonanser. Minst r har størst energi
For CO2 oppgis bare «Lower local quanta»; disse er knyttet til rotasjon
- Gren – Q, P, R.
- For Q er rotasjonskvantetallet uendret
- For P er rotasjonskvantetall 1 mindre i øvre nivå enn i nedre
- For R er rotasjonskvantetall 1 mer i øvre nivå enn i nedre
- Rotasjonskvantetall
- Symmetri – e og f
Se også DEL 2.
— Arne Marius Raaen —
