Pause i syntetiske data?

«Pausen» i global oppvarming er populær blant «skeptikere». F.eks. gir «Klimarealistene» oss en månedlig understreking av pausen.

Man bør strengt tatt skille mellom to typer pause: En reell endring i den underliggende globale oppvarmingen, eller en tilsynelatende «pause» fordi andre prosesser midlertidig motvirker den globale oppvarmingen. «Pausen» som IPPC beskriver er utvilsomt av den siste typen.

For å nærme seg dette, kan syntetiske data være nyttige – fordi man vet nøyaktig hvilken underliggende oppvarming som er lagt inn.

Figur 1 viser reelle troposfæriske data, RSS’ TLT 4.0.

Figur 2 viser et syntetisk datasett med samme stigningstall, med ukorrelert gaussisk støy med standardavvik 0,2. Det betyr at 95 % av utslagene ligger i intervallet -0,4 til 0,4 K.

Figur 1: RSS TLT 4.0, 480 måneder med data fra 1980. En standard linær regresjon gir et stigingstall som er svært når 2 K per århundre.

Figur 2: Syntetiske data med stigning 2 K per århundre, samt normalfordelt støy med standardavvik 0,2

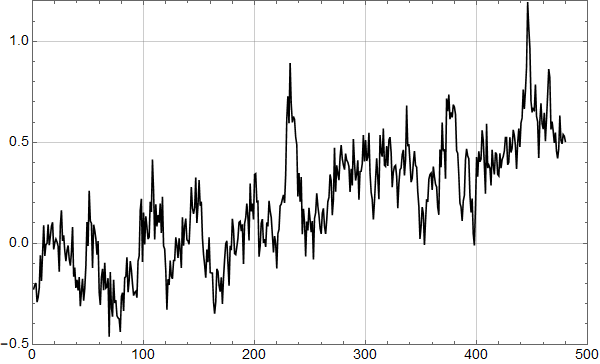
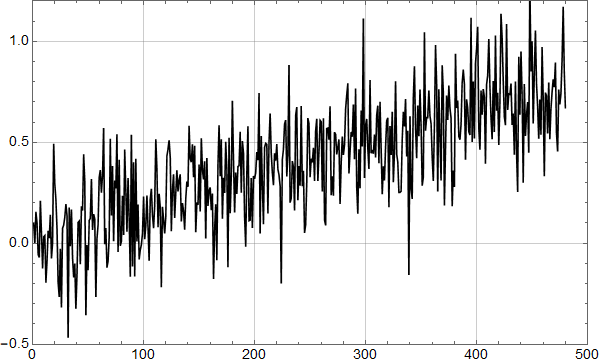
Det er helt klart at de to plottene er prinsipielt ulike, og det er klart hvorfor: I de reelle dataene er det en sammenheng mellom datapunktet en måned og den neste: Det er autokorrelasjon i dataene.

Vi trenger derfor en modell med autokorrelasjon. Den enkleste varianten er en såkalt AR(1) prosess: Verdien for en måned er korrelert med verdien for den forrige.

Figur 3 viser en sammenlikning mellom RSS dataene og et resultat fra slike syntetiske data.

Figur 3: Sammenlikning med RSS TLT 4.0 (svart) og syntetiske data (rødt). Den syntetiske er ikke tilfeldig valgt – den er den blant noen millioner realisasjoner som hadde minst kvadratisk avvik.

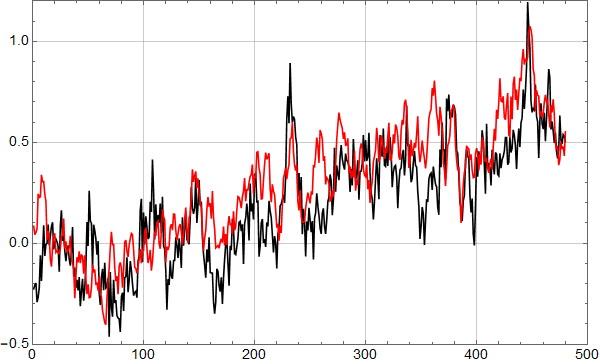
Vi har altså en prosess som genererer syntetiske data som ikke lenger har aldeles åpenbart avvik fra reelle temperatur data, og man kan tenke et det er mulig å analysere slike syntetiske data og si noe omtrentlig også om reelle data. Ikke til å trekke konklusjoner om reelle data, men å oppnå innsikter som kan brukes ved analyse av dem.

En fordel med syntetiske data er at man selv kan velge tidsrom. Figur 4 viser en realisasjon fra modellen over 400 år – 4800 måneder. Den dominerende underliggende stigningen vi har lagt inn blir veldig tydelig.

Figur 4: Eksempel på syntetiske data over 4800 måneder. Som forventet trer den dominerende trenden mye klarere fram.

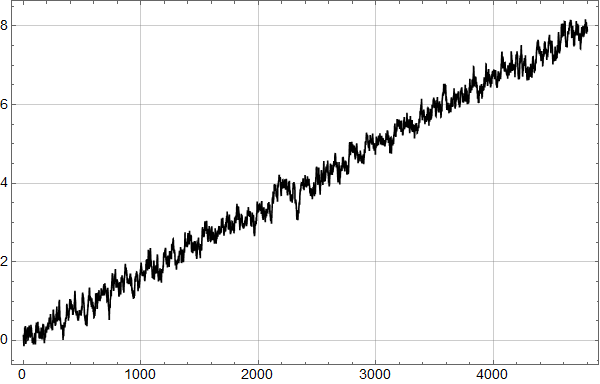
Vi kan også lett kjøre mange realisasjoner, og se på variasjonen vi får. Figur 5 viser resultatet av 10000 realisasjoner over 400 år i form av stigningstall beregnet med standard linær regresjon. Vi ser at de funne stigningstallene avviker lite fra det som er lagt inn i modellen: 2 K per århundre.

Figur 5: Spredning i stigningstall beregnet med linær regresjon for 10000 realisasjoner over 400 år. 95 % av verdiene ligger mellom 1,98 og 2,02.

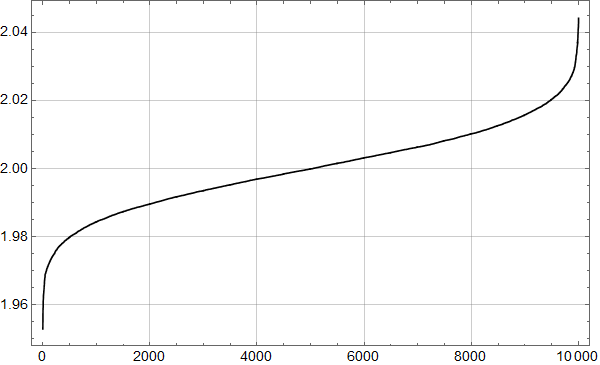
Ved å korte ned på tidsintervallet øker spredningen. Figur 6 viser resultat for 480 måneder, som er perioden vi har satellittdata for.

Figur 6: Spredning i stigningstall beregnet med lineær regresjon for 10000 realisasjoner over 40 år. 95 % av verdiene ligger mellom 1,27 og 2,71.

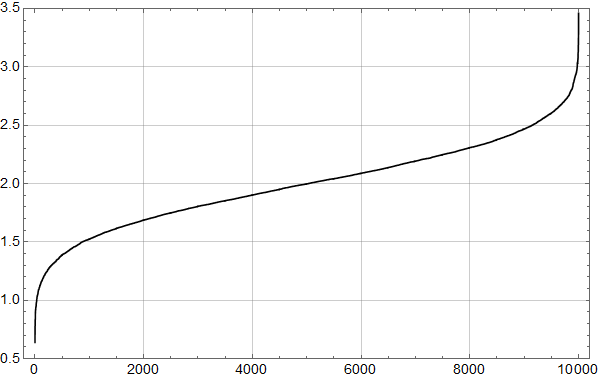
Altså: Selv om vi vet at de underliggende dataene har stigningstall på 2.0 K per århundre – de er jo hjemmelaget – fører støyen til at minste kvadraters metode gir atskillig variasjon mellom realisasjoner.

Til sist viser figur 7 resultatet for 180 måneder – 15 år.

Her har omtrent 1/3 av realisjonene et stigningstall som er mindre en halvparten av det som er lagt inn. Eller om man vil, minst en tredjedel av realisasjonene viser en «pause» – som vi vet ikke er der om vi snakker om den underliggende prosessen.

Figur 7: Spredning i stigningstall beregnet med linær regresjon for 10000 realisasjoner over 15 år. 95 % av verdiene ligger mellom -0,82 og 4,86.

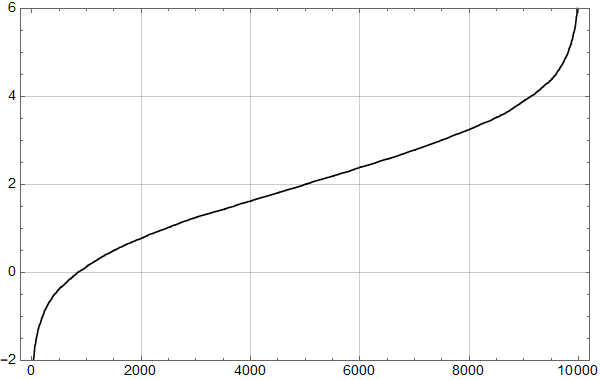
Litt lek med syntetiske data har lært oss noe om statistikken i tidsserier. Med en balanse mellom underliggende modellutvikling og støy som likner på det vi har i reelle data, ser vi at lengden på observasjonsperioden er viktig, og kan trekke en konklusjon:

Å tolke en pause i oppvarmingen basert på en 15-20 års periode har lite med vitenskap å gjøre – om man referer til den underliggende globale oppvarmingen.

Tillegg 6/9-2019

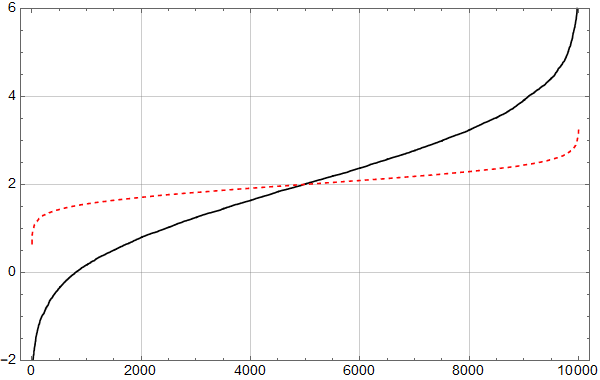
Det kan være instruktivt å plotte dataene i Figur 7 sammen med tilsvarende for ukorrelerte data. Resultatet er vist i Figur 8.

En ser at spredningen er atskillig mindre for data uten autokorrelasjon. Det betyr at om man bruker standardmetoder (som antar ukorrelert støy), som Excel’s LINEST, vil man undervurdere usikkerheten betydelig.

Figur 8: Spredning i stigningstall beregnet med linær regresjon for 10000 realisasjoner over 15 år, sammenliknet med tilsvarende for data uten autokorrelasjon (streket rød kurve). 95 % av verdiene ligger da mellom 1,32 og 2,68.

— Arne Marius Raaen —